题目内容
如图所示，在矩形ABCD中，AB=6，BC=8，将矩形折叠，使点C与点A重合，折痕为EF，再展平，EF与AC相交于点O，连接AF，CE，求折痕EF的长．考点：翻折变换（折叠问题）,矩形的性质
专题：
分析：将矩形折叠，使点C与点A重合，折痕为EF，则EF所在直线是线段AC的垂直平分线，根据AC与EF交于点O，则可以得出△AOE∽△ADC，求出OE的长，则EF=2OE．
解答：解：∵将矩形沿EF折叠，A，C重合，
∴∠AOE=∠D=90°，
又∵∠OAE=∠DAC，
∴△AOE∽△ADC，
∵AD=BC=8，CD=AB=6，
∴AC=
=10，
∴AO=5，
∴
=
，
∴
=
，
解得：EO=
，
∴EF=2EO=
．
故折痕EF的长为
．
∴∠AOE=∠D=90°，
又∵∠OAE=∠DAC，
∴△AOE∽△ADC，
∵AD=BC=8，CD=AB=6，
∴AC=
| AD2+CD2 |
∴AO=5，
∴
| AO |
| AD |
| EO |
| CD |
∴
| 5 |
| 8 |
| EO |
| 6 |
解得：EO=
| 15 |
| 4 |
∴EF=2EO=
| 15 |
| 2 |
故折痕EF的长为
| 15 |
| 2 |
点评：此题主要考查了翻折变换的性质，矩形的性质，勾股定理，相似三角形的判定与性质，证明△AOE∽△ADC是解题的关键．
练习册系列答案
相关题目
在实数5，
，
，
中，无理数是（ ）
| 3 |
| 7 |
| 2 |
| 4 |
| A、5 | ||
B、
| ||
C、
| ||
D、
|
已知矩形ABCD中，AB=60cm，BC=40cm，动点P从A点出发，沿着矩形的边自A→B→C→D运动到点D，速度为1m/s，设运动时间为 t（s），线段AP的长为y（cm），求此函数的解析式．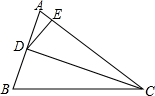
如图，已知CD是△ABC中∠ACB的角平分线，E是AC上的一点，且CD2=BC•CE，AD=6，AE=4．
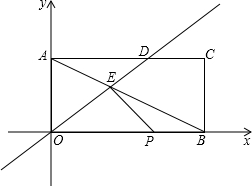如图，矩形AOBC在直角坐标系中，已知点A的坐标为（0，3），点B的坐标为（6，0），直线y=
如图，在平面直角坐标系种，点P在第一象限，⊙P与x轴相切于点Q，与y轴交于N（0，2），M（0，8）两点，反比例函数