题目内容
已知直线y=x+m与抛物线y=x2,从左至右依次交于A,B两点.
(1)求m的范围;
(2)若AB=3
,求△AOB.
(1)求m的范围;
(2)若AB=3
| 2 |
考点:二次函数的性质
专题:
分析:(1)直接将两函数联立得出关于x的方程,求出m得取值范围即可;
(2)利用两点距离公式,表示出AB的距离,进而求出m的值.
(2)利用两点距离公式,表示出AB的距离,进而求出m的值.
解答: 解:(1)由题意得:
解:(1)由题意得:
,
∴x2-x-m=0,
△=1+4m>0,
∴m>-
;
(2)当x2-x-m=0,
解得:xA=
,yA=
+m,
xB=
,yB=
+m,
∵AB=3
,
∴
=3
,
∴1+4m+1+4m=18,
解得:m=2,
∴xA=-1,xB=2,
∴S△AOB=
(xB-xA)m=
×3×2=3.
 解:(1)由题意得:
解:(1)由题意得:
|
∴x2-x-m=0,
△=1+4m>0,
∴m>-
| 1 |
| 4 |
(2)当x2-x-m=0,
解得:xA=
1-
| ||
| 2 |
1-
| ||
| 2 |
xB=
1+
| ||
| 2 |
1+
| ||
| 2 |
∵AB=3
| 2 |
∴
| (xB-xA)2+(yB-yA)2 |
| 2 |
∴1+4m+1+4m=18,
解得:m=2,
∴xA=-1,xB=2,
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了二次函数的性质以及三角形面积求法,表示出A,B点坐标是解题关键.

练习册系列答案
相关题目
2012年5月8日,“最美教师”张丽莉为救学生身负重伤,张老师舍己救人的事迹受到全国人民的极大关注,在住院期间,共有695万人以不同方式向她表示问候和祝福,将695万人用科学记数法表示为( )人.
| A、6.95×106 |
| B、6.95×105 |
| C、69.5×105 |
| D、69.5×106 |
若分式
的值为0,则x的值是( )
| x+3 |
| x |
| A、3 | B、-3 | C、0 | D、±3 |
 已知矩形ABCD中,AB=60cm,BC=40cm,动点P从A点出发,沿着矩形的边自A→B→C→D运动到点D,速度为1m/s,设运动时间为 t(s),线段AP的长为y(cm),求此函数的解析式.
已知矩形ABCD中,AB=60cm,BC=40cm,动点P从A点出发,沿着矩形的边自A→B→C→D运动到点D,速度为1m/s,设运动时间为 t(s),线段AP的长为y(cm),求此函数的解析式.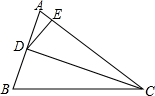 如图,已知CD是△ABC中∠ACB的角平分线,E是AC上的一点,且CD2=BC•CE,AD=6,AE=4.
如图,已知CD是△ABC中∠ACB的角平分线,E是AC上的一点,且CD2=BC•CE,AD=6,AE=4.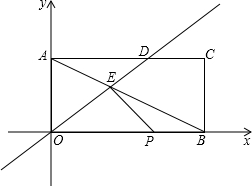 如图,矩形AOBC在直角坐标系中,已知点A的坐标为(0,3),点B的坐标为(6,0),直线y=
如图,矩形AOBC在直角坐标系中,已知点A的坐标为(0,3),点B的坐标为(6,0),直线y= 如图,已知∠AOC=∠BOD=100°,且∠AOB:∠AOD=2:7,试求∠BOC的大小.
如图,已知∠AOC=∠BOD=100°,且∠AOB:∠AOD=2:7,试求∠BOC的大小.