题目内容
9.已知一元二次方程x2-4x+3=0的两根x1、x2,则x12-4x1+x1x2=0.分析 由一元二次方程x2-4x+3=0的两根x1、x2可得x12-4x1=-3,x1x2=3,代入可得结果.
解答 解:∵一元二次方程x2-4x+3=0的两根x1、x2,
∴x12-4x1=-3,x1x2=3,
∴x12-4x1+x1x2=-3+3=0
故答案为:0.
点评 本题主要考查了一元二次方程根与系数的关系,关键是熟练掌握x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=$-\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
20.下列图形都是由同样大小的正方形和正三角形按一定的规律组成,其中,第①个图形中正方形和正三角形一共有5个,第②个图形中正方形和正三角形一共有13个,第③个图形中正方形和正三角形一共有26个,…,按此规律排列下去,第⑦个图形中正方形和正三角形个数一共有( )


| A. | 60个 | B. | 77个 | C. | 78个 | D. | 168个 |
17.用反证法证明:在四边形中,至少有一个内角大于或等于90°,应先假设( )
| A. | 四边形中每一个内角都小于90° | |
| B. | 四边形中最多有一个内角不小于90° | |
| C. | 四边形中每一个内角都大于90° | |
| D. | 四边形中有一个内角大于90° |
18.某房地产开发公司计划建A、B两种户型的住房共80套,且A户型不超过50套.已知该公司用于本次建房的资金不超过2096万元.两种户型的建房成本和售价如下表:
(1)试求该公司对建这两种户型住房套数的选定将有哪几种方案;
(2)试问该公司采取(1)中哪种方案建房,才能使获得的利润最大?最大利润为多少万元?
| 户型 | A | B |
| 成本(万元/套) | 25 | 28 |
| 售价(万元/套) | 30 | 34 |
(2)试问该公司采取(1)中哪种方案建房,才能使获得的利润最大?最大利润为多少万元?
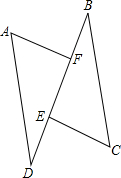 已知:如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,垂足分别为F、E,连接AD、BC,AD=CB,DE=BF,求证:AF=CE.
已知:如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,垂足分别为F、E,连接AD、BC,AD=CB,DE=BF,求证:AF=CE.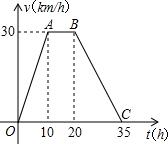 据某气象站观察和预测:发生于甲地的热带风暴正向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.
据某气象站观察和预测:发生于甲地的热带风暴正向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.