题目内容
1.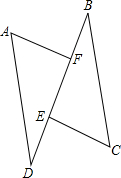 已知:如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,垂足分别为F、E,连接AD、BC,AD=CB,DE=BF,求证:AF=CE.
已知:如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,垂足分别为F、E,连接AD、BC,AD=CB,DE=BF,求证:AF=CE.
分析 利用已知条件证明△ADF≌△BCE,由全等三角形的性质即可得到AF=CE.
解答 证明:∵DE=BF,
∴DE+EF=BF+EF;
∴DF=BE;
在Rt△ADF和Rt△BCE中
$\left\{\begin{array}{l}{DF=BE}\\{AD=CB}\end{array}\right.$,
∴Rt△ADF≌Rt△BCE(HL),
∴AF=CE.
点评 本题考查了直角三角形全等的判定及性质;由DE=BF通过等量加等量和相等得DF=BE在三角形全等的证明中经常用到,应注意掌握应用.

练习册系列答案
相关题目
6.下列命题是假命题的是( )
| A. | 平行四边形的对角线互相平分 | B. | 平行四边形的对角相等 | ||
| C. | 平行四边形是轴对称图形 | D. | 平行四边形是中心对称图形 |
11.下列运算错误的是( )
| A. | ($\sqrt{3}$-1)0=1 | B. | (-3)2÷$\frac{9}{4}$=$\frac{1}{4}$ | C. | 5x2-6x2=-x2 | D. | (2m3)2÷(2m)2=m4 |
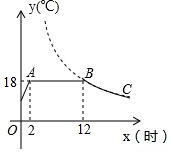 如图是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是反比例函数图象的一部分,则当x=20时,大棚内的温度约为10.8℃.
如图是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是反比例函数图象的一部分,则当x=20时,大棚内的温度约为10.8℃.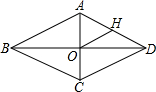 如图,菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为8,则OH的长等于1.
如图,菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为8,则OH的长等于1.