题目内容
18.某房地产开发公司计划建A、B两种户型的住房共80套,且A户型不超过50套.已知该公司用于本次建房的资金不超过2096万元.两种户型的建房成本和售价如下表:| 户型 | A | B |
| 成本(万元/套) | 25 | 28 |
| 售价(万元/套) | 30 | 34 |
(2)试问该公司采取(1)中哪种方案建房,才能使获得的利润最大?最大利润为多少万元?
分析 (1)A种房型的住房建x套,则B种房型建(80-x)套,根据题意得2090≤25x+28(80-x)≤2096,解不等式取整数值,即可求得方案.
(2)根据:利润=售价-成本,利润就可以写成关于x的函数,根据函数的性质,就可以求出函数的最大值.
解答 解:(1)设A种户型的住房建x套,则B种户型的住房建(80-x)套.
由题意,得2090≤25x+28(80-x)≤2096,
解得48≤x≤50.
因为x是整数,所以x为48,49,50,
故有三种建房方案:
方案一:建A型48套,建B型32套;
方案二:建A型49套,建B型31套;
方案三:建A型50套,建B型30套;
(2)设该公司建房获得利润为y万元.
则y=(30-25)x+(34-28)(80-x),
即y=480-x,
所以当x=48时,y最大=432.
即该公司建A型住房48套,B型住房32套可获得利润最大,最大利润是432万元.
点评 此题考查了一元一次不等式的应用与一次函数的实际应用.解题的关键是理解题意,注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
6.下列命题是假命题的是( )
| A. | 平行四边形的对角线互相平分 | B. | 平行四边形的对角相等 | ||
| C. | 平行四边形是轴对称图形 | D. | 平行四边形是中心对称图形 |
7.已知一元二次方程2x2-5x+1=0的两个根为x1,x2,下列结论正确的是( )
| A. | x1+x2=-$\frac{5}{2}$ | B. | x1•x2=1 | C. | x1,x2都是有理数 | D. | x1,x2都是正数 |
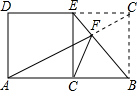 如图所示,在矩形ABCD中,∠DAC=65°,点E是CD上一点,BE交AC于点F,将△BCE沿BE折叠,点C恰好落在AB边上的点C′处,则∠AFC′=40°.
如图所示,在矩形ABCD中,∠DAC=65°,点E是CD上一点,BE交AC于点F,将△BCE沿BE折叠,点C恰好落在AB边上的点C′处,则∠AFC′=40°.