题目内容
17.用反证法证明:在四边形中,至少有一个内角大于或等于90°,应先假设( )| A. | 四边形中每一个内角都小于90° | |
| B. | 四边形中最多有一个内角不小于90° | |
| C. | 四边形中每一个内角都大于90° | |
| D. | 四边形中有一个内角大于90° |
分析 至少有一个角不小于90°的反面是每个角都小于90°,据此即可假设.
解答 解:用反证法证明:在四边形中,至少有一个角不小于90°,
应先假设:四边形中的每个角都小于90°.
故选:A.
点评 此题考查了反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
6.下列命题是假命题的是( )
| A. | 平行四边形的对角线互相平分 | B. | 平行四边形的对角相等 | ||
| C. | 平行四边形是轴对称图形 | D. | 平行四边形是中心对称图形 |
7.已知一元二次方程2x2-5x+1=0的两个根为x1,x2,下列结论正确的是( )
| A. | x1+x2=-$\frac{5}{2}$ | B. | x1•x2=1 | C. | x1,x2都是有理数 | D. | x1,x2都是正数 |
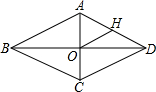 如图,菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为8,则OH的长等于1.
如图,菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为8,则OH的长等于1.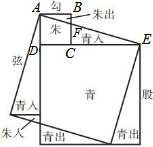 魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.
魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.