题目内容
已知：如图△ABC中，AB=AC，CD、BE是△ABC的角平分线.求证：AD=AE．
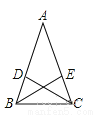
证明见解析.
【解析】试题分析：先根据CD、BE是△ABC的角平分线和等腰三角形的性质得到，∠1=∠2，∠A=∠A，结合AB=AC，可证△ADC≌△AEB，所以AD=AE．
试题解析：∵AB=AC（已知），
∴∠ABC=∠ACB．
∵CD、BE是△ABC的角平分线（已知），
∴∠1=∠ABC，∠2=∠ACB，
∴∠1=∠2．
又∵∠A=∠A（已知），
...
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
解分式方程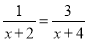
的解是________
-1
【解析】两边同时乘最简公分母（x+2）(x+4)整理成整式方程为：x+4=3x+6，解得x=-1，经检验是方程的解,故答案为：x=-1. 计算：
= ．
x．
【解析】
试题分析：===x．故答案为：x． 如图，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm速度向点A运动，点Q从点A同时出发以每秒2cm速度向点C运动，其中一个动点到达端点，另一个动点也随之停止，当△APQ是以PQ为底的等腰三角形时，运动的时间是( )秒
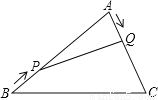
A. 2.5 B. 3 C. 3.5 D. 4
D
【解析】【解析】
设运动的时间为x，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动，当△APQ是等腰三角形时，AP=AQ，AP=20﹣3x，AQ=2x，即20﹣3x=2x，解得x=4．故选D． 如图，在等腰△ABC中，AB=AC，BD⊥AC，∠ABC=72°，则∠ABD=（ ）
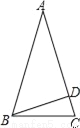
A. 36° B. 54° C. 18° D. 64°
B
【解析】试题分析：根据等腰三角形的性质由已知可求得∠A=36°，再根据垂直的定义和三角形内角和定理不难求得∠ABD=90°﹣36°=54°．
故选：B． 如图，在△ABC中，BC=5cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是 cm．
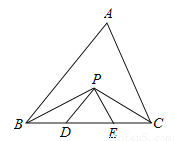
5．
【解析】
试题分析：∵BP、CP分别是∠ABC和∠ACB的角平分线，∴∠ABP=∠PBD，∠ACP=∠PCE，∵PD∥AB，PE∥AC，∴∠ABP=∠BPD，∠ACP=∠CPE，∴∠PBD=∠BPD，∠PCE=∠CPE，∴BD=PD，CE=PE，∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=5cm．故答案为：5． ∠AOB的平分线上一点M ，M到 OA的距离为1.5 cm，则M到OB的距离为_________。
1.5cm
【解析】∵M是∠AOB的平分线上一点，
∴点M到OB的距离等于M到OA的距离，
∴M到OB的距离为1.5cm.
故答案为：1.5cm. 某人乘雪橇沿如图所示的斜坡笔直下滑，滑下的距离s(m)与时间t(s)之间的关系式是s＝t2＋10t.若下滑的时间为2s，则此人下滑的高度是_______m.
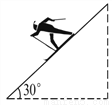
12
【解析】试题分析：把t＝2代入s＝ t2＋10t中得：
s＝24，
∵三角形是含30°角的直角三角形，
∴此人下滑的高度为：24×＝12米．
故答案为12． [（c·c2)+（a·a2)][（c·c2)-（a·a2)]等于（ ）
A. c3 -a3 B. c2 -a8 C. c5 -a5 D. c6 -a6
D
【解析】根据平方差公式和同底数幂的乘法法则可得：[（c·c2)+（a·a2)][（c·c2)-（a·a2)]= =c6 -a6，故选D.