题目内容
如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是( )秒
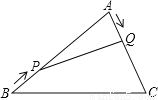
A. 2.5 B. 3 C. 3.5 D. 4
 D
【解析】【解析】
设运动的时间为x,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,当△APQ是等腰三角形时,AP=AQ,AP=20﹣3x,AQ=2x,即20﹣3x=2x,解得x=4.故选D.
D
【解析】【解析】
设运动的时间为x,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,当△APQ是等腰三角形时,AP=AQ,AP=20﹣3x,AQ=2x,即20﹣3x=2x,解得x=4.故选D.
练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
如图所示,四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是 ( )
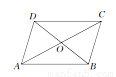
A. AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AO=CO,BO=DO
D. AB∥DC,AD=BC
 D
【解析】试题分析:A、根据两组对边分别平行的四边形为平行四边形;B、根据两组对边分别相等的四边形为平行四边形;C、根据对角线互相平分的四边形是平行四边形;D、不能判定.
D
【解析】试题分析:A、根据两组对边分别平行的四边形为平行四边形;B、根据两组对边分别相等的四边形为平行四边形;C、根据对角线互相平分的四边形是平行四边形;D、不能判定. 若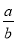 =
=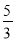 ,则
,则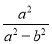 +
+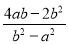 +
+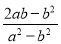 的值为( )
的值为( )
A. 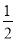 B.
B. 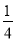 C. 2 D. 4
C. 2 D. 4
 B
【解析】++
=-+
=
=
=.
∵=,
∴设a=5k,b=3k,
∴原式==.
故选B.
B
【解析】++
=-+
=
=
=.
∵=,
∴设a=5k,b=3k,
∴原式==.
故选B. 如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.
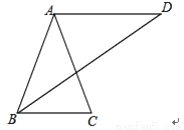
 证明见解析.
【解析】试题分析:首先根据AB=AC=AD,可得∠C=∠ABC,∠D=∠ABD,∠ABC=∠CBD+∠D;然后根据AD∥BC,可得∠CBD=∠D,据此判断出∠ABC=2∠D,再根据∠C=∠ABC,即可判断出∠C=2∠D.
试题解析:∵AB=AC=AD,
∴∠C=∠ABC,∠D=∠ABD.
∴∠ABC=∠CBD+∠D.
∵AD∥BC,
∴∠CBD=∠...
证明见解析.
【解析】试题分析:首先根据AB=AC=AD,可得∠C=∠ABC,∠D=∠ABD,∠ABC=∠CBD+∠D;然后根据AD∥BC,可得∠CBD=∠D,据此判断出∠ABC=2∠D,再根据∠C=∠ABC,即可判断出∠C=2∠D.
试题解析:∵AB=AC=AD,
∴∠C=∠ABC,∠D=∠ABD.
∴∠ABC=∠CBD+∠D.
∵AD∥BC,
∴∠CBD=∠... 等腰三角形的对称轴是______.
 顶角平分线所在直线
【解析】一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,如图所示:等腰三角形的对称轴是顶角平分线所在直线.
故答案是:顶角平分线所在直线.
顶角平分线所在直线
【解析】一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,如图所示:等腰三角形的对称轴是顶角平分线所在直线.
故答案是:顶角平分线所在直线. 如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( )

A.2 B.3 C.4 D.5
 D
【解析】
根据等腰三角形的性质可得AB=AC,继而得出AC的长.
【解析】
∵∠B=∠C,
∴AB=AC=5.
故选D.
D
【解析】
根据等腰三角形的性质可得AB=AC,继而得出AC的长.
【解析】
∵∠B=∠C,
∴AB=AC=5.
故选D. 已知:如图△ABC中,AB=AC,CD、BE是△ABC的角平分线.求证:AD=AE.
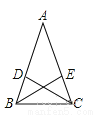
 证明见解析.
【解析】试题分析:先根据CD、BE是△ABC的角平分线和等腰三角形的性质得到,∠1=∠2,∠A=∠A,结合AB=AC,可证△ADC≌△AEB,所以AD=AE.
试题解析:∵AB=AC(已知),
∴∠ABC=∠ACB.
∵CD、BE是△ABC的角平分线(已知),
∴∠1=∠ABC,∠2=∠ACB,
∴∠1=∠2.
又∵∠A=∠A(已知),
...
证明见解析.
【解析】试题分析:先根据CD、BE是△ABC的角平分线和等腰三角形的性质得到,∠1=∠2,∠A=∠A,结合AB=AC,可证△ADC≌△AEB,所以AD=AE.
试题解析:∵AB=AC(已知),
∴∠ABC=∠ACB.
∵CD、BE是△ABC的角平分线(已知),
∴∠1=∠ABC,∠2=∠ACB,
∴∠1=∠2.
又∵∠A=∠A(已知),
... 如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,交AC于点D,若CD=n,AB=m,则△ABD的面积是( )
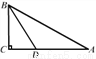
A. mn B. 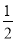 mn C. 2mn D.
mn C. 2mn D. 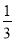 mn
mn
 B
【解析】
作DE⊥AB交AB于点E,
∵BD是∠ABC的平分线,∠C=90°,
∴CD=DE=n,
∴S△ABD=AB·DE=mn.
故选B.
B
【解析】
作DE⊥AB交AB于点E,
∵BD是∠ABC的平分线,∠C=90°,
∴CD=DE=n,
∴S△ABD=AB·DE=mn.
故选B. (2x-1)2等于( )
A. 4x2-4x+1 B. 2x2-2x+1 C. 2x2-1 D. 2x2+1
 A
【解析】根据完全平方公式可得:(2x-1)2=4x2-4x+1 ,故选A.
A
【解析】根据完全平方公式可得:(2x-1)2=4x2-4x+1 ,故选A. 
