题目内容
如图，在等腰△ABC中，AB=AC，BD⊥AC，∠ABC=72°，则∠ABD=（ ）
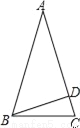
A. 36° B. 54° C. 18° D. 64°
B
【解析】试题分析：根据等腰三角形的性质由已知可求得∠A=36°，再根据垂直的定义和三角形内角和定理不难求得∠ABD=90°﹣36°=54°．
故选：B．
练习册系列答案
相关题目
“五一”江北水城文化旅游节期间，几名同学包租一辆面包车前去旅游，面包车的租价为180元，出发时又增加了两名同学，结果每个同学比原来少摊了3元钱车费，设参加游览的同学共x人，应该如何列出方程？（不用求解，只列出即可）
【解析】分析：设原来参加游览的同学共x人，面包车的租价为180元，出发时又增加了两名同学，结果每个同学比原来少摊了3元钱车费，可列方程．
本题解析：设参加游览的同学共x人，那么出发前为x—2人，
根据题意可以得出 化简： 
＋
－
＝___.
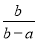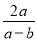－1
【解析】试题解析：原式
故答案为： 等腰三角形的对称轴是______．
顶角平分线所在直线
【解析】一个图形沿一条直线对折，直线两旁的部分能够完全重合，那么这个图形就是轴对称图形，这条直线就是这个图形的一条对称轴,如图所示：等腰三角形的对称轴是顶角平分线所在直线.
故答案是：顶角平分线所在直线. 在△ABC中，∠ACB=90°，BE平分∠ABC，ED⊥AB于D．如果∠A=30°，AE=6cm，那么CE等于（ ）
A. 4 cm B. 2 cm C. 3 cm D. 1 cm
C
【解析】∵ED⊥AB，∠A=30°，
∴AE=2ED，
∵AE=6cm，
∴ED=3cm.
∵∠ACB=90°，BE平分∠ABC，
∴ED=CE，
∴CE=3cm.
故选C. 已知：如图△ABC中，AB=AC，CD、BE是△ABC的角平分线.求证：AD=AE．
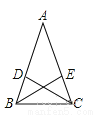
证明见解析.
【解析】试题分析：先根据CD、BE是△ABC的角平分线和等腰三角形的性质得到，∠1=∠2，∠A=∠A，结合AB=AC，可证△ADC≌△AEB，所以AD=AE．
试题解析：∵AB=AC（已知），
∴∠ABC=∠ACB．
∵CD、BE是△ABC的角平分线（已知），
∴∠1=∠ABC，∠2=∠ACB，
∴∠1=∠2．
又∵∠A=∠A（已知），
... 如图，△ABC中，∠C=90°，AD平分∠BAC，交BC于D，若DC=7，则点D到AB的距离DE= ．
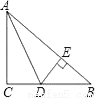
7
【解析】试题分析： ∵∠C=90°，AD平分∠BAC，点D到AB的距离DE，∴DE=DC=7．故填7． 如图，有一个长为24米的篱笆，一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S平方米．
(1)求S与x的函数关系式及x的取值范围；
(2)如果要围成面积为45平方米的花圃，那么AB的长为多少米？
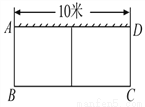
(1)S＝－3x2＋24x(≤x＜8)；（2）5米
【解析】试题分析：
（1）可先用x表示出BC的长，然后根据矩形的面积＝长×宽，得出S与x的函数关系式．根据墙的最大可用长度为10米求出自变量的取值范围；
（2）根据（1）的函数关系式，将S＝45代入其中，求出x的值即可．
试题解析：
【解析】
（1）由题可知，花圃的宽AB为x米，则BC为（24－3x）米．
这... 102×98等于_______；
9996
【解析】102×98=（100+2）×（100-2）=10000-4=9996.