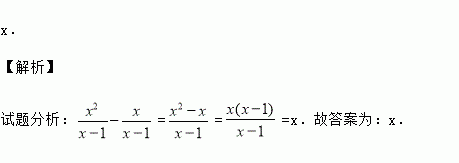题目内容
计算: = .
= .
 x.
【解析】
试题分析:===x.故答案为:x.
x.
【解析】
试题分析:===x.故答案为:x.
练习册系列答案
相关题目
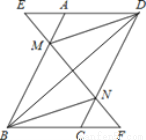
如图所示,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:BD与MN互相平分.
 (1)证明见解析(2)证明见解析
【解析】试题分析:(1)先根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAM=∠FCN,从而利用ASA可作出证明;
(2)根据平行四边形的性质及(1)的结论可得BM 平行且等于DN,则由有一组对边平行且相等的四边形是平行四边形可得四边形BMDN是平行四边形,再由平行四边形的性质即可证明结论....
(1)证明见解析(2)证明见解析
【解析】试题分析:(1)先根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAM=∠FCN,从而利用ASA可作出证明;
(2)根据平行四边形的性质及(1)的结论可得BM 平行且等于DN,则由有一组对边平行且相等的四边形是平行四边形可得四边形BMDN是平行四边形,再由平行四边形的性质即可证明结论.... 下面是分式方程的是( )
A. 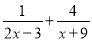 B.
B. 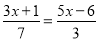
C. 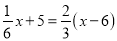 D.
D. 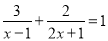
 D
【解析】A、不是方程,故本选项错误;
B、分母中不含有未知数,是整式方程,故本选项错误;
C、分母中不含有未知数,是整式方程,故本选项错误;
D、分母中含有未知数,是分式方程,故本选项正确.
故选D.
D
【解析】A、不是方程,故本选项错误;
B、分母中不含有未知数,是整式方程,故本选项错误;
C、分母中不含有未知数,是整式方程,故本选项错误;
D、分母中含有未知数,是分式方程,故本选项正确.
故选D. 若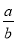 =
=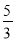 ,则
,则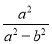 +
+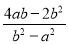 +
+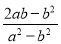 的值为( )
的值为( )
A. 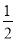 B.
B. 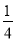 C. 2 D. 4
C. 2 D. 4
 B
【解析】++
=-+
=
=
=.
∵=,
∴设a=5k,b=3k,
∴原式==.
故选B.
B
【解析】++
=-+
=
=
=.
∵=,
∴设a=5k,b=3k,
∴原式==.
故选B. 化简:  +
+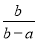 -
-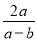 =___.
=___.
 -1
【解析】试题解析:原式
故答案为:
-1
【解析】试题解析:原式
故答案为: 如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.
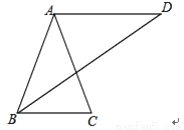
 证明见解析.
【解析】试题分析:首先根据AB=AC=AD,可得∠C=∠ABC,∠D=∠ABD,∠ABC=∠CBD+∠D;然后根据AD∥BC,可得∠CBD=∠D,据此判断出∠ABC=2∠D,再根据∠C=∠ABC,即可判断出∠C=2∠D.
试题解析:∵AB=AC=AD,
∴∠C=∠ABC,∠D=∠ABD.
∴∠ABC=∠CBD+∠D.
∵AD∥BC,
∴∠CBD=∠...
证明见解析.
【解析】试题分析:首先根据AB=AC=AD,可得∠C=∠ABC,∠D=∠ABD,∠ABC=∠CBD+∠D;然后根据AD∥BC,可得∠CBD=∠D,据此判断出∠ABC=2∠D,再根据∠C=∠ABC,即可判断出∠C=2∠D.
试题解析:∵AB=AC=AD,
∴∠C=∠ABC,∠D=∠ABD.
∴∠ABC=∠CBD+∠D.
∵AD∥BC,
∴∠CBD=∠... 等腰三角形的对称轴是______.
 顶角平分线所在直线
【解析】一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,如图所示:等腰三角形的对称轴是顶角平分线所在直线.
故答案是:顶角平分线所在直线.
顶角平分线所在直线
【解析】一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,如图所示:等腰三角形的对称轴是顶角平分线所在直线.
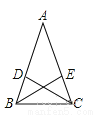
故答案是:顶角平分线所在直线. 已知:如图△ABC中,AB=AC,CD、BE是△ABC的角平分线.求证:AD=AE.
 证明见解析.
【解析】试题分析:先根据CD、BE是△ABC的角平分线和等腰三角形的性质得到,∠1=∠2,∠A=∠A,结合AB=AC,可证△ADC≌△AEB,所以AD=AE.
试题解析:∵AB=AC(已知),
∴∠ABC=∠ACB.
∵CD、BE是△ABC的角平分线(已知),
∴∠1=∠ABC,∠2=∠ACB,
∴∠1=∠2.
又∵∠A=∠A(已知),
...
证明见解析.
【解析】试题分析:先根据CD、BE是△ABC的角平分线和等腰三角形的性质得到,∠1=∠2,∠A=∠A,结合AB=AC,可证△ADC≌△AEB,所以AD=AE.
试题解析:∵AB=AC(已知),
∴∠ABC=∠ACB.
∵CD、BE是△ABC的角平分线(已知),
∴∠1=∠ABC,∠2=∠ACB,
∴∠1=∠2.
又∵∠A=∠A(已知),
... (3a-4b)2等于_______;
 9a2-24ab+16b2
【解析】根据完全平方公式可得:(3a-4b)2=9a2-24ab+16b2.
9a2-24ab+16b2
【解析】根据完全平方公式可得:(3a-4b)2=9a2-24ab+16b2.