题目内容
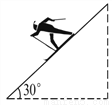
某人乘雪橇沿如图所示的斜坡笔直下滑,滑下的距离s(m)与时间t(s)之间的关系式是s=t2+10t.若下滑的时间为2s,则此人下滑的高度是_______m.
 12
【解析】试题分析:把t=2代入s= t2+10t中得:
s=24,
∵三角形是含30°角的直角三角形,
∴此人下滑的高度为:24×=12米.
故答案为12.
12
【解析】试题分析:把t=2代入s= t2+10t中得:
s=24,
∵三角形是含30°角的直角三角形,
∴此人下滑的高度为:24×=12米.
故答案为12.
练习册系列答案
相关题目
若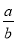 =
=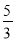 ,则
,则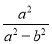 +
+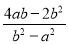 +
+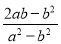 的值为( )
的值为( )
A. 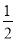 B.
B. 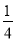 C. 2 D. 4
C. 2 D. 4
 B
【解析】++
=-+
=
=
=.
∵=,
∴设a=5k,b=3k,
∴原式==.
故选B.
B
【解析】++
=-+
=
=
=.
∵=,
∴设a=5k,b=3k,
∴原式==.
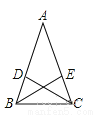
故选B. 已知:如图△ABC中,AB=AC,CD、BE是△ABC的角平分线.求证:AD=AE.
 证明见解析.
【解析】试题分析:先根据CD、BE是△ABC的角平分线和等腰三角形的性质得到,∠1=∠2,∠A=∠A,结合AB=AC,可证△ADC≌△AEB,所以AD=AE.
试题解析:∵AB=AC(已知),
∴∠ABC=∠ACB.
∵CD、BE是△ABC的角平分线(已知),
∴∠1=∠ABC,∠2=∠ACB,
∴∠1=∠2.
又∵∠A=∠A(已知),
...
证明见解析.
【解析】试题分析:先根据CD、BE是△ABC的角平分线和等腰三角形的性质得到,∠1=∠2,∠A=∠A,结合AB=AC,可证△ADC≌△AEB,所以AD=AE.
试题解析:∵AB=AC(已知),
∴∠ABC=∠ACB.
∵CD、BE是△ABC的角平分线(已知),
∴∠1=∠ABC,∠2=∠ACB,
∴∠1=∠2.
又∵∠A=∠A(已知),
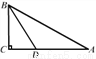
... 如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,交AC于点D,若CD=n,AB=m,则△ABD的面积是( )
A. mn B. 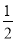 mn C. 2mn D.
mn C. 2mn D. 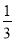 mn
mn
 B
【解析】
作DE⊥AB交AB于点E,
∵BD是∠ABC的平分线,∠C=90°,
∴CD=DE=n,
∴S△ABD=AB·DE=mn.
故选B.
B
【解析】
作DE⊥AB交AB于点E,
∵BD是∠ABC的平分线,∠C=90°,
∴CD=DE=n,
∴S△ABD=AB·DE=mn.
故选B. 如图,有一个长为24米的篱笆,一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式及x的取值范围;
(2)如果要围成面积为45平方米的花圃,那么AB的长为多少米?
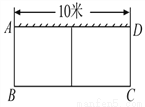
 (1)S=-3x2+24x(≤x<8);(2)5米
【解析】试题分析:
(1)可先用x表示出BC的长,然后根据矩形的面积=长×宽,得出S与x的函数关系式.根据墙的最大可用长度为10米求出自变量的取值范围;
(2)根据(1)的函数关系式,将S=45代入其中,求出x的值即可.
试题解析:
【解析】
(1)由题可知,花圃的宽AB为x米,则BC为(24-3x)米.
这...
(1)S=-3x2+24x(≤x<8);(2)5米
【解析】试题分析:
(1)可先用x表示出BC的长,然后根据矩形的面积=长×宽,得出S与x的函数关系式.根据墙的最大可用长度为10米求出自变量的取值范围;
(2)根据(1)的函数关系式,将S=45代入其中,求出x的值即可.
试题解析:
【解析】
(1)由题可知,花圃的宽AB为x米,则BC为(24-3x)米.
这... (3a-b)(3a+b)-(2a-b)2
 5a2+4ab-2b2
【解析】试题分析:先根据平方差公式与完全平方公式分别计算,再合并同类项即可.
试题解析:
(3a-b)(3a+b)-(2a-b)2=9a2-b2-4a2+4ab-b2=5a2+4ab-2b2.
5a2+4ab-2b2
【解析】试题分析:先根据平方差公式与完全平方公式分别计算,再合并同类项即可.
试题解析:
(3a-b)(3a+b)-(2a-b)2=9a2-b2-4a2+4ab-b2=5a2+4ab-2b2. (3a-4b)2等于_______;
 9a2-24ab+16b2
【解析】根据完全平方公式可得:(3a-4b)2=9a2-24ab+16b2.
9a2-24ab+16b2
【解析】根据完全平方公式可得:(3a-4b)2=9a2-24ab+16b2. (2x-1)2等于( )
A. 4x2-4x+1 B. 2x2-2x+1 C. 2x2-1 D. 2x2+1
 A
【解析】根据完全平方公式可得:(2x-1)2=4x2-4x+1 ,故选A.
A
【解析】根据完全平方公式可得:(2x-1)2=4x2-4x+1 ,故选A. 小明、小宇从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小宇骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小明出发时间t(分)之间的函数关系如图所示.下列说法:①小宇先到达青少年宫;②小宇的速度是小明速度的3倍;③a=20;④b=600.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
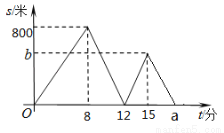
 B.
【解析】
试题分析:由图象得出小文步行720米,需要9分钟,
所以小文的运动速度为:720÷9=80(m/分),
当第15分钟时,小亮运动15-9=6(分钟),
运动距离为:15×80=1200(m),
∴小亮的运动速度为:1200÷6=200(m/分),
∴200÷80=2.5,(故②正确);
当第19分钟以后两人之间距离越来越近,说明小亮已...
B.
【解析】
试题分析:由图象得出小文步行720米,需要9分钟,
所以小文的运动速度为:720÷9=80(m/分),
当第15分钟时,小亮运动15-9=6(分钟),
运动距离为:15×80=1200(m),
∴小亮的运动速度为:1200÷6=200(m/分),
∴200÷80=2.5,(故②正确);
当第19分钟以后两人之间距离越来越近,说明小亮已... 
