题目内容
解分式方程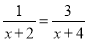 的解是________
的解是________
 -1
【解析】两边同时乘最简公分母(x+2)(x+4)整理成整式方程为:x+4=3x+6,解得x=-1,经检验是方程的解,故答案为:x=-1.
-1
【解析】两边同时乘最简公分母(x+2)(x+4)整理成整式方程为:x+4=3x+6,解得x=-1,经检验是方程的解,故答案为:x=-1.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
光明机械厂生产一批新产品,由一班、二班合作,原计划6天完成,但是,他们合作了4天后,二班被调走了,一班对做了6天才全部做完,那么一班、二班单独做各需要几天完成?
 一班单独完成需要18天,二班单独完成需要9天.
【解析】试题分析:设一班单独做需要x天完成,则一班的工作效率为,二班的工作效率为,根据工作效率工作时间=工作总量列出方程求解即可.
试题解析:设一班单独做需要x天完成,则一班的工作效率为,二班的工作效率为,
依题意得,
解得x=18,经检验知当x=18时,符合题意.∴=9,
答:一班单独完成需要18天,二班单独完成需要9...
一班单独完成需要18天,二班单独完成需要9天.
【解析】试题分析:设一班单独做需要x天完成,则一班的工作效率为,二班的工作效率为,根据工作效率工作时间=工作总量列出方程求解即可.
试题解析:设一班单独做需要x天完成,则一班的工作效率为,二班的工作效率为,
依题意得,
解得x=18,经检验知当x=18时,符合题意.∴=9,
答:一班单独完成需要18天,二班单独完成需要9... 如图所示,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:BD与MN互相平分.
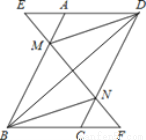
 (1)证明见解析(2)证明见解析
【解析】试题分析:(1)先根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAM=∠FCN,从而利用ASA可作出证明;
(2)根据平行四边形的性质及(1)的结论可得BM 平行且等于DN,则由有一组对边平行且相等的四边形是平行四边形可得四边形BMDN是平行四边形,再由平行四边形的性质即可证明结论....
(1)证明见解析(2)证明见解析
【解析】试题分析:(1)先根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAM=∠FCN,从而利用ASA可作出证明;
(2)根据平行四边形的性质及(1)的结论可得BM 平行且等于DN,则由有一组对边平行且相等的四边形是平行四边形可得四边形BMDN是平行四边形,再由平行四边形的性质即可证明结论.... 如图所示,四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是 ( )
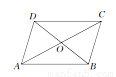
A. AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AO=CO,BO=DO
D. AB∥DC,AD=BC
 D
【解析】试题分析:A、根据两组对边分别平行的四边形为平行四边形;B、根据两组对边分别相等的四边形为平行四边形;C、根据对角线互相平分的四边形是平行四边形;D、不能判定.
D
【解析】试题分析:A、根据两组对边分别平行的四边形为平行四边形;B、根据两组对边分别相等的四边形为平行四边形;C、根据对角线互相平分的四边形是平行四边形;D、不能判定. “五一”江北水城文化旅游节期间,几名同学包租一辆面包车前去旅游,面包车的租价为180元,出发时又增加了两名同学,结果每个同学比原来少摊了3元钱车费,设参加游览的同学共x人,应该如何列出方程?(不用求解,只列出即可)
 【解析】分析:设原来参加游览的同学共x人,面包车的租价为180元,出发时又增加了两名同学,结果每个同学比原来少摊了3元钱车费,可列方程.
本题解析:设参加游览的同学共x人,那么出发前为x—2人,
根据题意可以得出
【解析】分析:设原来参加游览的同学共x人,面包车的租价为180元,出发时又增加了两名同学,结果每个同学比原来少摊了3元钱车费,可列方程.
本题解析:设参加游览的同学共x人,那么出发前为x—2人,
根据题意可以得出 已知关于x的分式方程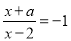 的根大于零,那么a的取值范围是_____________
的根大于零,那么a的取值范围是_____________
 a<2且a≠-2
【解析】方程两边都乘(x-2)得,x+a=2-x,
解得x=.∵根大于0, ∴>0, ∴a<2, ∵x-2≠0, ∴-2≠0,
解得:a≠-2, ∴a的取值范围是a<2且a≠-2.故答案为: a<2且a≠-2.
a<2且a≠-2
【解析】方程两边都乘(x-2)得,x+a=2-x,
解得x=.∵根大于0, ∴>0, ∴a<2, ∵x-2≠0, ∴-2≠0,
解得:a≠-2, ∴a的取值范围是a<2且a≠-2.故答案为: a<2且a≠-2. 下面是分式方程的是( )
A. 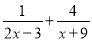 B.
B. 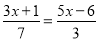
C. 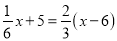 D.
D. 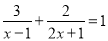
 D
【解析】A、不是方程,故本选项错误;
B、分母中不含有未知数,是整式方程,故本选项错误;
C、分母中不含有未知数,是整式方程,故本选项错误;
D、分母中含有未知数,是分式方程,故本选项正确.
故选D.
D
【解析】A、不是方程,故本选项错误;
B、分母中不含有未知数,是整式方程,故本选项错误;
C、分母中不含有未知数,是整式方程,故本选项错误;
D、分母中含有未知数,是分式方程,故本选项正确.
故选D. 若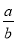 =
=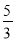 ,则
,则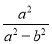 +
+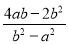 +
+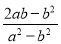 的值为( )
的值为( )
A. 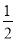 B.
B. 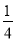 C. 2 D. 4
C. 2 D. 4
 B
【解析】++
=-+
=
=
=.
∵=,
∴设a=5k,b=3k,
∴原式==.
故选B.
B
【解析】++
=-+
=
=
=.
∵=,
∴设a=5k,b=3k,
∴原式==.
故选B. 已知:如图△ABC中,AB=AC,CD、BE是△ABC的角平分线.求证:AD=AE.
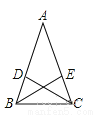
 证明见解析.
【解析】试题分析:先根据CD、BE是△ABC的角平分线和等腰三角形的性质得到,∠1=∠2,∠A=∠A,结合AB=AC,可证△ADC≌△AEB,所以AD=AE.
试题解析:∵AB=AC(已知),
∴∠ABC=∠ACB.
∵CD、BE是△ABC的角平分线(已知),
∴∠1=∠ABC,∠2=∠ACB,
∴∠1=∠2.
又∵∠A=∠A(已知),
...
证明见解析.
【解析】试题分析:先根据CD、BE是△ABC的角平分线和等腰三角形的性质得到,∠1=∠2,∠A=∠A,结合AB=AC,可证△ADC≌△AEB,所以AD=AE.
试题解析:∵AB=AC(已知),
∴∠ABC=∠ACB.
∵CD、BE是△ABC的角平分线(已知),
∴∠1=∠ABC,∠2=∠ACB,
∴∠1=∠2.
又∵∠A=∠A(已知),
... 
