题目内容
7.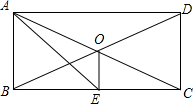 如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=$\frac{1}{4}$BC;④S△ACE=$\frac{1}{8}$S?ABCD.其中正确的个数是( )
如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=$\frac{1}{4}$BC;④S△ACE=$\frac{1}{8}$S?ABCD.其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由矩形的性质得出∠BAD=∠ABC=90°,OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,OB=OC,由等腰三角形的性质得出BE=CE,OE⊥BC,OE=$\frac{1}{2}$AB,证出△ABE是等腰直角三角形,得出AB=BE=$\frac{1}{2}$BC,得出①不正确,②、③正确;由△ACE的面积=$\frac{1}{4}$矩形ABCD的面积,得出④不正确;即可得出结论.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OB=OC,
∵E是BC的中点,
∴BE=CE,OE⊥BC,OE=$\frac{1}{2}$AB,
∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE=$\frac{1}{2}$BC,
∴OE=$\frac{1}{4}$BC,tan∠ACB=$\frac{AB}{BC}$=$\frac{1}{2}$≠$\frac{\sqrt{3}}{3}$,
∴∠ACB≠30°,
∴①不正确,②、③正确;
∵△ACE的面积=$\frac{1}{2}$CE•AB=$\frac{1}{2}$×$\frac{1}{2}$BC•AB=$\frac{1}{4}$BC•AB=$\frac{1}{4}$矩形ABCD的面积,
∴④不正确;正确的有2个,
故选:B.
点评 本题考查了矩形的性质、等腰三角形的性质、等腰直角三角形的判定与性质、三角函数、三角形面积的计算;熟练掌握矩形的性质,证明三角形是等腰直角三角形是解决问题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
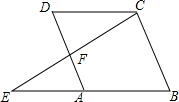 如图,?ABCD中,点E在BA的延长线上,CE交AD于F,求证:$\frac{DC}{BE}$=$\frac{DF}{BC}$.
如图,?ABCD中,点E在BA的延长线上,CE交AD于F,求证:$\frac{DC}{BE}$=$\frac{DF}{BC}$.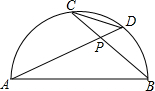 如图,以AB为直径的半圆O,CD为弦,连结AD,BC.
如图,以AB为直径的半圆O,CD为弦,连结AD,BC. 如图,在?ABCD中,对角线AC、BD相交于点O.如果AC=8,BD=14,AB=x,那么x的取值范围是3<x<11.
如图,在?ABCD中,对角线AC、BD相交于点O.如果AC=8,BD=14,AB=x,那么x的取值范围是3<x<11. 如图,在矩形ABCD中,E、F分别是AD、BC中点,连接AF、BE、CE、DF分别交于点M、N,四边形EMFN是菱形.
如图,在矩形ABCD中,E、F分别是AD、BC中点,连接AF、BE、CE、DF分别交于点M、N,四边形EMFN是菱形.
 如图所示,在?ABCD中,BF⊥AD于F,BE⊥CD于E,若∠A=60°,AF=3cm,CE=2cm,则?ABCD的周长为20cm..
如图所示,在?ABCD中,BF⊥AD于F,BE⊥CD于E,若∠A=60°,AF=3cm,CE=2cm,则?ABCD的周长为20cm..