题目内容
16.分式$\frac{x}{x^3}、\frac{3a+1}{3a+b}、\frac{m+n}{{{m^2}-{n^2}}}、\frac{2-2x}{2x}$中,最简分式的个数是1个.分析 最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
解答 解:$\frac{x}{x^3}、\frac{3a+1}{3a+b}、\frac{m+n}{{{m^2}-{n^2}}}、\frac{2-2x}{2x}$中最简分式是$\frac{3a+1}{3a+b}$,
故答案为:1
点评 此题主要考查了最简分式,分式的化简过程,首先要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
8.能判定四边形ABCD为平行四边形的题设是( )
| A. | AB∥CD,AD=BC | B. | AB∥CD,∠A=∠C | C. | ∠A=∠B,∠C=∠D | D. | AB=CD,∠D=∠B |
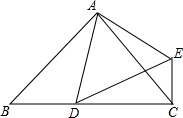 已知:如图,$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$.
已知:如图,$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$.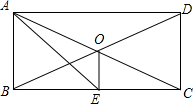 如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=$\frac{1}{4}$BC;④S△ACE=$\frac{1}{8}$S?ABCD.其中正确的个数是( )
如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=$\frac{1}{4}$BC;④S△ACE=$\frac{1}{8}$S?ABCD.其中正确的个数是( )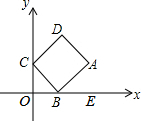 如图,矩形ABCD的顶点A的坐标为(4,2),顶点B,C分别在x轴,y轴的正半轴上
如图,矩形ABCD的顶点A的坐标为(4,2),顶点B,C分别在x轴,y轴的正半轴上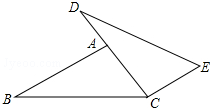 如图,点D、A、C在同一直线上,AB∥CE,AB=CD,∠B=∠D,求证:BC=DE.
如图,点D、A、C在同一直线上,AB∥CE,AB=CD,∠B=∠D,求证:BC=DE.