题目内容
17.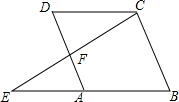 如图,?ABCD中,点E在BA的延长线上,CE交AD于F,求证:$\frac{DC}{BE}$=$\frac{DF}{BC}$.
如图,?ABCD中,点E在BA的延长线上,CE交AD于F,求证:$\frac{DC}{BE}$=$\frac{DF}{BC}$.
分析 根据平行四边形的性质的AD∥BC,CD∥AB,根据相似三角形的性质得到$\frac{AF}{BC}=\frac{AE}{BE}$,$\frac{CD}{AE}=\frac{DF}{AF}$,根据比例的性质得到$\frac{BE}{BC}=\frac{AE}{AF}$,$\frac{CD}{DF}=\frac{AE}{AF}$,等量代换得到$\frac{BE}{BC}=\frac{CD}{DF}$,再根据比例的性质即可得到结论.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,CD∥AB,
∴△AEF∽△BEC,△CDF∽△AEF,
∴$\frac{AF}{BC}=\frac{AE}{BE}$,$\frac{CD}{AE}=\frac{DF}{AF}$,
∴$\frac{BE}{BC}=\frac{AE}{AF}$,$\frac{CD}{DF}=\frac{AE}{AF}$,
∴$\frac{BE}{BC}=\frac{CD}{DF}$,
∴$\frac{DC}{BE}$=$\frac{DF}{BC}$.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,比例的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
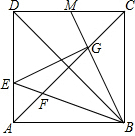 如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.
如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.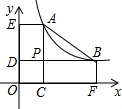 如图,点A,B在双曲线y=$\frac{k}{x}$(x>0)上,分别过点A、B向x轴、y轴作垂线.垂足分别为点C、E、F、D,AC和BD交于点P,$\frac{AP}{PC}$=2且△ABP的面积为4,有以下结论:
如图,点A,B在双曲线y=$\frac{k}{x}$(x>0)上,分别过点A、B向x轴、y轴作垂线.垂足分别为点C、E、F、D,AC和BD交于点P,$\frac{AP}{PC}$=2且△ABP的面积为4,有以下结论: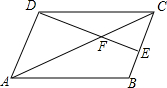 如图,四边形ABCD是平行四边形,E为BC边的中点,DE、AC相交于点F,若△CEF的面积为6,则四边形ABEF的面积为30.
如图,四边形ABCD是平行四边形,E为BC边的中点,DE、AC相交于点F,若△CEF的面积为6,则四边形ABEF的面积为30.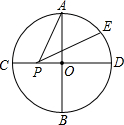 如图,AB与CD是半径为1的⊙O互相垂直的两直径,E为弧AD的三等分点(点E距点D近),P是直径CD上一动点,则PA+PE的最小值为$\sqrt{3}$.
如图,AB与CD是半径为1的⊙O互相垂直的两直径,E为弧AD的三等分点(点E距点D近),P是直径CD上一动点,则PA+PE的最小值为$\sqrt{3}$.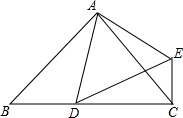 已知:如图,$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$.
已知:如图,$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$.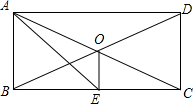 如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=$\frac{1}{4}$BC;④S△ACE=$\frac{1}{8}$S?ABCD.其中正确的个数是( )
如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=$\frac{1}{4}$BC;④S△ACE=$\frac{1}{8}$S?ABCD.其中正确的个数是( )