题目内容
2. 如图,在矩形ABCD中,E、F分别是AD、BC中点,连接AF、BE、CE、DF分别交于点M、N,四边形EMFN是菱形.
如图,在矩形ABCD中,E、F分别是AD、BC中点,连接AF、BE、CE、DF分别交于点M、N,四边形EMFN是菱形.
分析 求出四边形ABFE为平行四边形,四边形BFDE为平行四边形,根据平行四边形的性质得出BE∥FD,即ME∥FN,同理可证EN∥MF,得出四边形EMFN为平行四边形,求出ME=MF,根据菱形的判定得出即可.
解答 解:四边形EMFN是菱形;理由如下:
∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
又∵E,F分别为AD,BC中点,
∴AE∥BF,AE=BF,ED∥CF,DE=CF,
∴四边形ABFE为平行四边形,四边形BFDE为平行四边形,
∴BE∥FD,即ME∥FN,
同理可证EN∥MF,
∴四边形EMFN为平行四边形,
∵四边形ABFE为平行四边形,∠ABC为直角,
∴ABFE为矩形,
∴AF,BE互相平分于M点,
∴ME=MF,
∴四边形EMFN为菱形;
故答案为:菱形.
点评 本题考查了矩形的性质和判定,菱形的判定,平行四边形的性质和判定的应用,能综合运用性质进行推理是解此题的关键,题目比较好,综合性比较强.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
14.已知四点A(0,-2),B(1,0),C(2,2),D(0,4),若一个二次函数的图象经过这四点中的三点,则这个二次函数图象的对称轴为( )
| A. | x=$\frac{7}{6}$ | B. | x=-$\frac{7}{6}$ | C. | x=-$\frac{6}{7}$ | D. | x=$\frac{6}{7}$ |
 已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.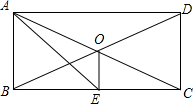 如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=$\frac{1}{4}$BC;④S△ACE=$\frac{1}{8}$S?ABCD.其中正确的个数是( )
如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=$\frac{1}{4}$BC;④S△ACE=$\frac{1}{8}$S?ABCD.其中正确的个数是( )