题目内容
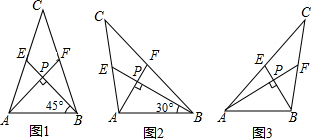
12.我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P.像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.特例探索
(1)①如图1,当∠ABE=45°,$c=2\sqrt{2}$时,a=2$\sqrt{5}$,b=2$\sqrt{5}$;
②如图2,当∠ABE=30°,c=4时,求a和b的值
归纳证明
(2)请你观察(1)中的计算结果,猜想三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
分析 (1)先判断△ABP是等腰直角三角形,再得到△EFP也是等腰直角三角形,最后计算即可;
(2)先设AP=m,BP=n,表示出线段PE,PF,最后利用勾股定理即可.
解答 解:(1)①当∠ABE=45°,$c=2\sqrt{2}$时,a=$2\sqrt{5}$,b=$2\sqrt{5}$
如图1,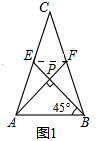
连接EF,则EF是△ABC的中位线
∴EF=$\frac{1}{2}AB$=$\sqrt{2}$,
∵∠ABE=45°,AE⊥EF
∴△ABP是等腰直角三角形,
∵EF∥AB,
∴△EFP也是等腰直角三角形,
∴AP=BP=2,EP=FP=1,
∴AE=BF=$\sqrt{5}$,
∴.$a=b=2\sqrt{5}$
②如图2,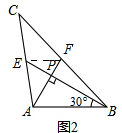
连接EF,则EF是△ABC的中位线.
∵∠ABE=30°,AE⊥BF,AB=4,
∴AP=2,BP=$2\sqrt{3}$,
∵EF∥AB,EF=$\frac{1}{2}$AB,PE=$\sqrt{3}$,PF=1
∴AE=$\sqrt{7}$,BF=$\sqrt{13}$
∴$a=2\sqrt{13}$,$b=2\sqrt{7}$.
(2)a2+b2=5c2
如图3,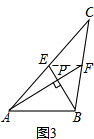
连接EF,设AP=m,BP=n,
则c2=AB2=m2+n2,
∵EF∥AB,EF=$\frac{1}{2}$AB,
∴PE=$\frac{1}{2}$BP=$\frac{1}{2}$n,PF=$\frac{1}{2}$AP=$\frac{1}{2}$m,
∴$A{E^2}={m^2}+\frac{1}{4}{n^2}$,$B{F^2}={n^2}+\frac{1}{4}{m^2}$,
∴b2=AC2=4AE2=4m2+n2,a2=BC2=4BF2=4n2+m2
∴a2+b2=5(m2+n2)=5c2.
点评 此题是三角形综合题,主要考查了等腰三角形的性质和判定,勾股定理,三角形的中位线,表示出线段是解本题的关键.

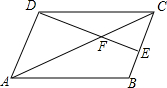 如图,四边形ABCD是平行四边形,E为BC边的中点,DE、AC相交于点F,若△CEF的面积为6,则四边形ABEF的面积为30.
如图,四边形ABCD是平行四边形,E为BC边的中点,DE、AC相交于点F,若△CEF的面积为6,则四边形ABEF的面积为30.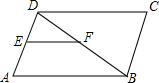 如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为7.
如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为7.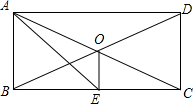 如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=$\frac{1}{4}$BC;④S△ACE=$\frac{1}{8}$S?ABCD.其中正确的个数是( )
如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=$\frac{1}{4}$BC;④S△ACE=$\frac{1}{8}$S?ABCD.其中正确的个数是( )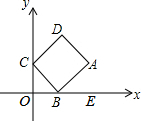 如图,矩形ABCD的顶点A的坐标为(4,2),顶点B,C分别在x轴,y轴的正半轴上
如图,矩形ABCD的顶点A的坐标为(4,2),顶点B,C分别在x轴,y轴的正半轴上