题目内容
18.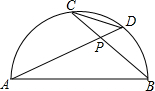 如图,以AB为直径的半圆O,CD为弦,连结AD,BC.
如图,以AB为直径的半圆O,CD为弦,连结AD,BC.(1)若∠APC=60°,求△CPD与△APB的面积之比.
(2)若CD=3.5,AB=7,BC=5,求PC的长.
分析 (1)连接AC,由圆周角定理得出∠ACB=90°,证出∠CAD=30°,由三角函数得出$\frac{PC}{PA}$=$\frac{1}{2}$,证出△CPD∽△APB,由相似三角形的性质即可得出结果;
(2)由相似三角形的性质得出$\frac{CD}{AB}$=$\frac{PC}{PA}$=$\frac{1}{2}$,由勾股定理求出AC,由三角函数求出PC即可.
解答 解:(1)连接AC,如图所示: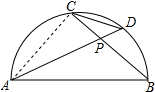
∵AB是直径,
∴∠ACB=90°,
∵∠APC=60°,
∴∠CAD=30°
∴sin∠CAD=$\frac{1}{2}$,
∵sin∠CAD=$\frac{PC}{PA}$,
∴$\frac{PC}{PA}$=$\frac{1}{2}$,
∵∠ADC=∠ABC,∠CPD=∠APB,
∴△CPD∽△APB,
∴$\frac{{S}_{△CPD}}{{S}_{△APB}}$=($\frac{PC}{PA}$)2=$\frac{1}{4}$;
(2)∵△CPD∽△APB,
∴$\frac{CD}{AB}$=$\frac{PC}{PA}$=$\frac{1}{2}$,
由勾股定理得:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{7}^{2}-{5}^{2}}$=2$\sqrt{6}$,
在Rt△ACP中,PC=tan∠CAP•AC=tan30°•AC=$\frac{\sqrt{3}}{3}$×2$\sqrt{6}$=2$\sqrt{2}$.
点评 本题考查了圆周角定理、相似三角形的判定由V型在、三角函数等知识;熟练掌握圆周角定理,证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
8.能判定四边形ABCD为平行四边形的题设是( )
| A. | AB∥CD,AD=BC | B. | AB∥CD,∠A=∠C | C. | ∠A=∠B,∠C=∠D | D. | AB=CD,∠D=∠B |
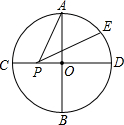 如图,AB与CD是半径为1的⊙O互相垂直的两直径,E为弧AD的三等分点(点E距点D近),P是直径CD上一动点,则PA+PE的最小值为$\sqrt{3}$.
如图,AB与CD是半径为1的⊙O互相垂直的两直径,E为弧AD的三等分点(点E距点D近),P是直径CD上一动点,则PA+PE的最小值为$\sqrt{3}$.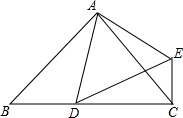 已知:如图,$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$.
已知:如图,$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$.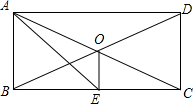 如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=$\frac{1}{4}$BC;④S△ACE=$\frac{1}{8}$S?ABCD.其中正确的个数是( )
如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=$\frac{1}{4}$BC;④S△ACE=$\frac{1}{8}$S?ABCD.其中正确的个数是( )