题目内容
5.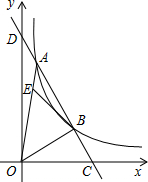 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )| A. | k=$\frac{7}{2}$S | B. | k=3S | C. | k=$\frac{8}{3}$S | D. | k=$\frac{5}{2}$S |
分析 作AM⊥OC于M,BN⊥OC于N,根据反比例函数系数k的几何意义得到S△AOM=S△BON,于是得到S△AOB=S梯形AMNB,设B(m,$\frac{k}{m}$),根据平行线分线段成比例定理得到$\frac{BC}{AC}=\frac{BN}{AM}$=$\frac{1}{3}$,求得A($\frac{m}{3}$,$\frac{3k}{m}$),根据OE=3EA,△AEB的面积为S,得到S△AOB=4S=$\frac{1}{2}$($\frac{k}{m}$+$\frac{3k}{m}$)×(m-$\frac{m}{3}$),于是得到结论.
解答 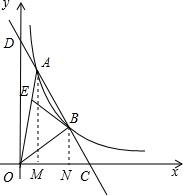 解:作AM⊥OC于M,BN⊥OC于N,
解:作AM⊥OC于M,BN⊥OC于N,
∵S△AOM=S△BON,
∴S△AOB=S梯形AMNB,
设B(m,$\frac{k}{m}$),
∵AM∥BN,∴$\frac{BC}{AC}=\frac{BN}{AM}$=$\frac{1}{3}$,
∴A($\frac{m}{3}$,$\frac{3k}{m}$),
∵OE=3EA,△AEB的面积为S,∴S△AOB=4S=$\frac{1}{2}$($\frac{k}{m}$+$\frac{3k}{m}$)×(m-$\frac{m}{3}$),
∴4S=$\frac{4k}{3}$,
∴k=3S,
故选B.
点评 本题考查了反比例函数和一次函数的交点,反比例函数系数k的几何意义,根据反比例函数系数k的几何意义得出S△AOB=S梯形AMNB是解题的关键.

练习册系列答案
相关题目
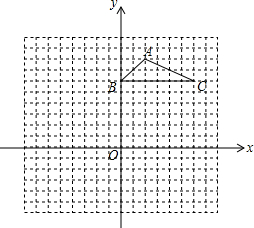 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图所示的平面直角坐标系.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图所示的平面直角坐标系.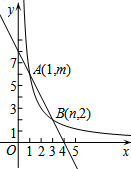 直线y=-2x+8和双曲线y=$\frac{k}{x}$(k≠0)交于点A(1,m),B(n,2).
直线y=-2x+8和双曲线y=$\frac{k}{x}$(k≠0)交于点A(1,m),B(n,2).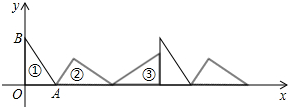 如图①,在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为($\frac{144}{5}$,$\frac{12}{5}$).
如图①,在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为($\frac{144}{5}$,$\frac{12}{5}$).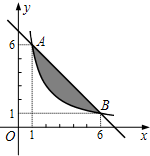 如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y=$\frac{k}{x}$(x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为3个.
如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y=$\frac{k}{x}$(x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为3个.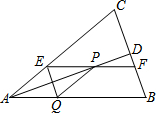 如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交
如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交