题目内容
13.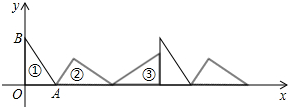 如图①,在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为($\frac{144}{5}$,$\frac{12}{5}$).
如图①,在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为($\frac{144}{5}$,$\frac{12}{5}$).
分析 根据勾股定理列式求出AB的长度,再利用面积法计算图②的直角顶点的纵坐标,然后根据图形不难发现,每3个图形为一个循环组依次循环,所以图⑧与图②的直角顶点的纵坐标相同,横坐标为两个三角形周长加OH的长.
解答  解:∵∠AOB=90°,OA=3,OB=4,
解:∵∠AOB=90°,OA=3,OB=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
过C作CH⊥x轴于H,如图,
∵$\frac{1}{2}$CH•5=$\frac{1}{2}$•3•4,
∴CH=$\frac{12}{5}$,
∴AH=$\sqrt{{3}^{2}-(\frac{12}{5})^{2}}$=$\frac{9}{5}$,
根据图形,每3个图形为一个循环组,3+5+4=12,
而8=3×2+2,
∴图⑧与图②的直角顶点的纵坐标相同,都为$\frac{12}{5}$,图⑧的直角顶点的横坐标为2×12+3+$\frac{9}{5}$=$\frac{144}{5}$,
即图⑧的直角顶点的坐标为($\frac{144}{5}$,$\frac{12}{5}$).
故答案为($\frac{144}{5}$,$\frac{12}{5}$).
点评 本题考查了坐标与图形变换:旋转图形的坐标:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.也考查了勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.在四张完全相同的卡片上,分别画有等边三角形、菱形、正五边形、圆.现从中随机抽取一张,卡片上的图形恰好是中心对称图形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
5.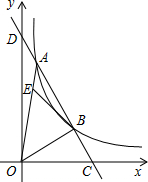 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )| A. | k=$\frac{7}{2}$S | B. | k=3S | C. | k=$\frac{8}{3}$S | D. | k=$\frac{5}{2}$S |
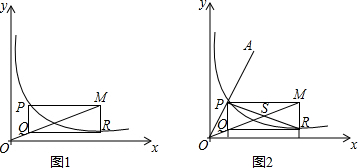
3. 如图所示的是由一些正方体小木块搭成的几何体的主视图与俯视图,它最多需要小木块的块数是( )
如图所示的是由一些正方体小木块搭成的几何体的主视图与俯视图,它最多需要小木块的块数是( )
 如图所示的是由一些正方体小木块搭成的几何体的主视图与俯视图,它最多需要小木块的块数是( )
如图所示的是由一些正方体小木块搭成的几何体的主视图与俯视图,它最多需要小木块的块数是( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
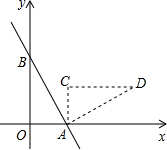 如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△ACD,则点D的坐标是(7,3).
如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△ACD,则点D的坐标是(7,3).