题目内容
10.已知x为整数且满足不等式组$\left\{\begin{array}{l}{3x-2>7}\\{6-2x>-4}\end{array}\right.$,求$\frac{2x}{{x}^{2}-4}$÷($\frac{{x}^{2}}{x-2}$-x)的值.分析 先算括号里面的,再算除法,求出不等式的解集,选取合适的x的值代入进行计算即可.
解答 解:原式=$\frac{2x}{(x+2)(x-2)}$÷$\frac{{x}^{2}-x(x-2)}{x-2}$
=$\frac{2x}{(x+2)(x-2)}$÷$\frac{{x}^{2}-{x}^{2}+2x}{x-2}$
=$\frac{2x}{(x+2)(x-2)}$•$\frac{x-2}{2x}$
=$\frac{1}{x+2}$.
解不等式组$\left\{\begin{array}{l}3x-2>7①\\ 6-2x>-4②\end{array}\right.$得,3<x<5,
∴当x=4时,原式=$\frac{1}{4+2}$=$\frac{1}{6}$.
点评 本题考查的是分式的化简求值,在解答此类问题时注意x的取值保证分式有意义.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
20.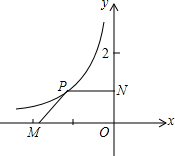 如图,平面直角坐标系中,点M是x轴负半轴上一定点,点P是函数y=-$\frac{1}{x}$,(x<0)上一动点,PN⊥y轴于点N,当点P的横坐标在逐渐增大时,四边形PMON的面积将会( )
如图,平面直角坐标系中,点M是x轴负半轴上一定点,点P是函数y=-$\frac{1}{x}$,(x<0)上一动点,PN⊥y轴于点N,当点P的横坐标在逐渐增大时,四边形PMON的面积将会( )
 如图,平面直角坐标系中,点M是x轴负半轴上一定点,点P是函数y=-$\frac{1}{x}$,(x<0)上一动点,PN⊥y轴于点N,当点P的横坐标在逐渐增大时,四边形PMON的面积将会( )
如图,平面直角坐标系中,点M是x轴负半轴上一定点,点P是函数y=-$\frac{1}{x}$,(x<0)上一动点,PN⊥y轴于点N,当点P的横坐标在逐渐增大时,四边形PMON的面积将会( )| A. | 逐渐增大 | B. | 始终不变 | C. | 逐渐减小 | D. | 先增后减 |
18.在四张完全相同的卡片上,分别画有等边三角形、菱形、正五边形、圆.现从中随机抽取一张,卡片上的图形恰好是中心对称图形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
5.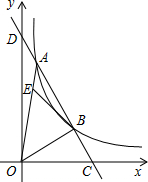 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )| A. | k=$\frac{7}{2}$S | B. | k=3S | C. | k=$\frac{8}{3}$S | D. | k=$\frac{5}{2}$S |
19.下表记录了小敏等四名学生五次数学测验成绩的平均数与方差:
根据表中数据,要从中挑选一名成绩好又比较稳定的同学参加我区的数学头脑运动会,你认为应该选( )
| 衡量指标 | 小敏 | 小芳 | 小聪 | 小明 |
| 平均数 | 90 | 85 | 90 | 85 |
| 方差 | 3 | 3 | 10 | 12 |
| A. | 小明 | B. | 小芳 | C. | 小聪 | D. | 小敏 |
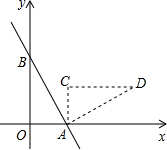 如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△ACD,则点D的坐标是(7,3).
如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△ACD,则点D的坐标是(7,3). 如图,在?ABCD中,连接BD,BD⊥BC,CD=4,sinC=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.
如图,在?ABCD中,连接BD,BD⊥BC,CD=4,sinC=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.