题目内容
16.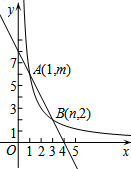 直线y=-2x+8和双曲线y=$\frac{k}{x}$(k≠0)交于点A(1,m),B(n,2).
直线y=-2x+8和双曲线y=$\frac{k}{x}$(k≠0)交于点A(1,m),B(n,2).(1)求m,n,k的值;
(2)在坐标轴上有一点M,使MA+MB的值最小,直接写出点M的坐标.
分析 (1)由于点A(1,m),B(n,2)在直线y=-2x+8上,于是得到方程m=-2+8,2=-2n+8,即可得到结论;
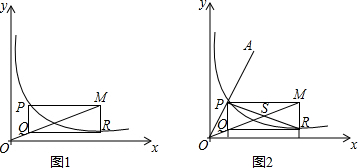
(2)如图1,作点A关于y轴的对称点C,连接BC交y轴与M,求得C(-1,6),求出直线BC的解析式为y=-2x+5,得到M(0,5);如图2,作点A关于x轴的对称点D,连接BD交x轴与M,得到D(1,-6),求出直线BD的解析式为y=4x-10,得到M($\frac{5}{2}$,0).
解答  解:(1)∵点A(1,m),B(n,2)在直线y=-2x+8上,
解:(1)∵点A(1,m),B(n,2)在直线y=-2x+8上,
∴m=-2+8,2=-2n+8,
∴m=6,n=3
∴A(1,6),B(3,2),
∵点A在双曲线y=$\frac{k}{x}$(k≠0)上,
∴k=6;
(2)如图1,作点A关于y轴的对称点C,连接BC交y轴与M,
则C(-1,6),
设直线BC的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{6=-k+b}\\{2=3k+b}\end{array}\right.$,∴$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$,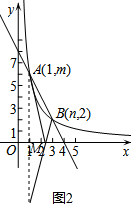
∴直线BC的解析式为y=-x+5,
∴M(0,5);
∴AM+BM=$\sqrt{2}$+3$\sqrt{2}$=4$\sqrt{2}$;
如图2,作点A关于x轴的对称点D,连接BD交x轴与M,
则D(1,-6),
设直线BD的解析式为y=mx+n,
∴$\left\{\begin{array}{l}{-6=m+n}\\{2=3m+n}\end{array}\right.$,∴$\left\{\begin{array}{l}{m=4}\\{n=-10}\end{array}\right.$,
∴直线BD的解析式为y=4x-10,
当y=0时,x=$\frac{5}{2}$,
∴M($\frac{5}{2}$,0).
∴AM+BM=$\frac{\sqrt{17}}{2}$+$\frac{3\sqrt{17}}{2}$=2$\sqrt{17}$>4$\sqrt{2}$,
∴M(0,5).
点评 本题考查了反比例函数与一次函数的交点,坐标与图形变化-对称轴对称-最短路线问题,注意待定系数法求直线解析式的运用,有一定的难度.

| A. | 1+(1-x)=1 | B. | 1-(1-x)=1 | C. | 1+(1-x)=x-3 | D. | 1-(1-x)=x-3 |
 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,相反数最大的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,相反数最大的是( )| A. | a | B. | b | C. | c | D. | d |
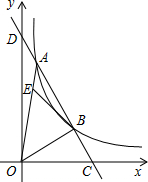 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )| A. | k=$\frac{7}{2}$S | B. | k=3S | C. | k=$\frac{8}{3}$S | D. | k=$\frac{5}{2}$S |
 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )| A. | a | B. | b | C. | c | D. | d |