题目内容
14.关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;②(m-1)2+(n-1)2≥2;③-1≤2m-2n≤1,其中正确结论的个数是3个.分析 ①根据题意,以及根与系数的关系,可知两个整数根都是负数;②根据根的判别式,以及题意可以得出m2-2n≥0以及n2-2m≥0,进而得解;③可以采用根与系数关系进行解答,据此即可得解.
解答 解:①两个整数根且乘积为正,两个根同号,由韦达定理有,x1•x2=2n>0,y1•y2=2m>0,
y1+y2=-2n<0,
x1+x2=-2m<0,
这两个方程的根都为负根,①正确;
②由根判别式有:
△=b2-4ac=4m2-8n≥0,△=b2-4ac=4n2-8m≥0,
∵4m2-8n≥0,4n2-8m≥0,
∴m2-2n≥0,n2-2m≥0,
m2-2m+1+n2-2n+1=m2-2n+n2-2m+2≥2,
(m-1)2+(n-1)2≥2,②正确;
③由根与系数关系可得2m-2n=y1y2+y1+y2=(y1+1)(y2+1)-1,
由y1、y2均为负整数,故(y1+1)•(y2+1)≥0,故2m-2n≥-1,
同理可得:2n-2m=x1x2+x1+x2=(x1+1)(x2+1)-1,得2n-2m≥-1,即2m-2n≤1,故③正确,
故答案为:3个.
点评 本题主要考查了根与系数的关系,以及一元二次方程的根的判别式,根据不同结论灵活运用根与系数的关系是难点.

练习册系列答案
相关题目
5.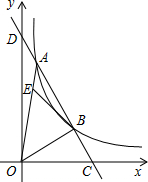 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )| A. | k=$\frac{7}{2}$S | B. | k=3S | C. | k=$\frac{8}{3}$S | D. | k=$\frac{5}{2}$S |
19.下表记录了小敏等四名学生五次数学测验成绩的平均数与方差:
根据表中数据,要从中挑选一名成绩好又比较稳定的同学参加我区的数学头脑运动会,你认为应该选( )
| 衡量指标 | 小敏 | 小芳 | 小聪 | 小明 |
| 平均数 | 90 | 85 | 90 | 85 |
| 方差 | 3 | 3 | 10 | 12 |
| A. | 小明 | B. | 小芳 | C. | 小聪 | D. | 小敏 |
6. 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )| A. | a | B. | b | C. | c | D. | d |
3. 如图所示的是由一些正方体小木块搭成的几何体的主视图与俯视图,它最多需要小木块的块数是( )
如图所示的是由一些正方体小木块搭成的几何体的主视图与俯视图,它最多需要小木块的块数是( )
 如图所示的是由一些正方体小木块搭成的几何体的主视图与俯视图,它最多需要小木块的块数是( )
如图所示的是由一些正方体小木块搭成的几何体的主视图与俯视图,它最多需要小木块的块数是( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
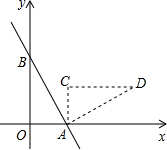 如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△ACD,则点D的坐标是(7,3).
如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△ACD,则点D的坐标是(7,3).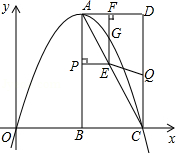 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8),抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8),抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E.