题目内容
20.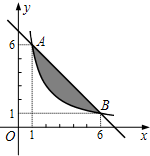 如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y=$\frac{k}{x}$(x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为3个.
如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y=$\frac{k}{x}$(x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为3个.
分析 先利用待定系数法求得反比例函数的解析式为y=$\frac{6}{x}$;直线AB的解析式为y=-x+7;然后分别把x=2、3、4、5代入两个解析式,分别求出对应的纵坐标,再易得到图中阴影部分(不包括边界)所含格点的坐标.
解答 解:把A(1,6)代入y=$\frac{k}{x}$,得k=1×6=6,
∴反比例函数的解析式为y=$\frac{6}{x}$;
设直线AB的解析式为y=ax+b,
把A(1,6),B(6,1)代入得,ax+b=6,a+b=1,解得a=-1,b=7,
∴直线AB的解析式为y=-x+7;
当x=2,y=$\frac{6}{x}$=3;y=-x+7=5;
当x=3,y=$\frac{6}{x}$=2;y=-x+7=4;
当x=4,y=$\frac{6}{x}$=$\frac{3}{2}$;y=-x+7=3;
当x=5,y=$\frac{6}{x}$=$\frac{6}{5}$;y=-x+7=2,
∴图中阴影部分(不包括边界)所含格点的有:(2,4),(3,3),(4,2),
故答案为3.
点评 本题考查了待定系数法求反比例函数和一次函数的解析式.也考查了横纵坐标都为整数的点的坐标的确定方法.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
10.在一个不透明的口袋中装有5个质地、大小、颜色完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号不大于3的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
11. 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,相反数最大的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,相反数最大的是( )
 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,相反数最大的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,相反数最大的是( )| A. | a | B. | b | C. | c | D. | d |
5.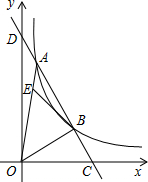 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )| A. | k=$\frac{7}{2}$S | B. | k=3S | C. | k=$\frac{8}{3}$S | D. | k=$\frac{5}{2}$S |
12. 学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
(1)表中 m=,15; n=0.4.
(2)根据表中数据,求出B类同学数所对应的圆心角的度数.
(3)学校在开展了解校训意义活动中,需要将D类的甲、乙、丙、丁四名同学分成两组,每两人一组,求D类4个人中甲乙两人分成一组的概率是多少?(请用列表法或是树状图表示)
 学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:| 类别 | A | B | C | D |
| 频数 | 20 | m | 11 | 4 |
| 频率 | n | 0.3 | 0.22 | 0.08 |
(2)根据表中数据,求出B类同学数所对应的圆心角的度数.
(3)学校在开展了解校训意义活动中,需要将D类的甲、乙、丙、丁四名同学分成两组,每两人一组,求D类4个人中甲乙两人分成一组的概率是多少?(请用列表法或是树状图表示)