题目内容
15. 如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )
如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{5}$ |
分析 设AE=$\frac{1}{2}$AB=1,CF=x,则AB=BF=2,CE=CB=1+x,在Rt△BCF中,根据勾股定理可得x2+22=(1+x)2,即可得到CB的长,最后在Rt△BCF中,根据cos∠CBF=$\frac{BF}{BC}$进行计算即可.
解答  解:设AE=$\frac{1}{2}$AB=1,CF=x,则AB=BF=2,
解:设AE=$\frac{1}{2}$AB=1,CF=x,则AB=BF=2,
由折叠可得,∠AEB=∠FEB,∠EFB=∠A=90°,
由AD∥BC可得,∠CBE=∠AEB,
∴∠CBE=∠CEB,
∴CE=CB=1+x,
在Rt△BCF中,CF2+BF2=BC2,
∴x2+22=(1+x)2,
解得x=$\frac{3}{2}$,
∴CE=1+x=$\frac{5}{2}$,
∴CB=$\frac{5}{2}$,
∴Rt△BCF中,cos∠CBF=$\frac{BF}{BC}$=$\frac{2}{\frac{5}{2}}$=$\frac{4}{5}$.
故选:B.
点评 本题主要考查了折叠问题,勾股定理,解直角三角形以及矩形的性质的运用,解决问题的方法是设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
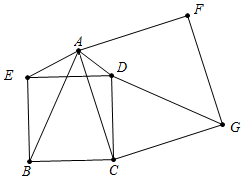 如图,BCDE,ACGF是正方形,三角形AED、CDG的面积分别为4.5与8,那么正方形BCDE的面积是多少?
如图,BCDE,ACGF是正方形,三角形AED、CDG的面积分别为4.5与8,那么正方形BCDE的面积是多少?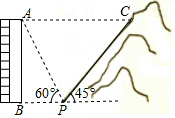 图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
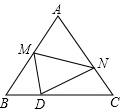 如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为7或$\frac{65}{3}$.
如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为7或$\frac{65}{3}$.