题目内容
10.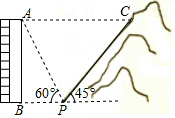 图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.(1)求居民楼AB的高度;
(2)求C、A之间的距离.(结果保留根号)
分析 (1)首先分析图形:根据题意构造直角三角形,利用在Rt△CPE中,由sin45°=$\frac{CE}{PC}$,得出EC的长度,进而可求出答案.
(2)在Rt△ABP中,利用tan60°=$\frac{AB}{BP}$,得出BP的长,进而得出PE的长,即可得出答案.
解答 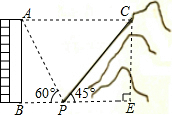 解:(1)如图,过点C作CE⊥BP于点E,
解:(1)如图,过点C作CE⊥BP于点E,
在Rt△CPE中,∵PC=30m,∠CPE=45°,
∴sin45°=$\frac{CE}{PC}$,
∴CE=PC•sin45°=30×$\frac{\sqrt{2}}{2}$=15$\sqrt{2}$m,
∵点C与点A在同一水平线上,
∴AB=CE=15$\sqrt{2}$m,
答:居民楼AB的高度为15$\sqrt{2}$m;
(2)在Rt△ABP中,∵∠APB=60°,
∴tan60°=$\frac{AB}{BP}$,
∴BP=$\frac{15\sqrt{2}}{\sqrt{3}}$=5$\sqrt{6}$m,
∵PE=CE=15$\sqrt{2}$m,
∴AC=BE=15$\sqrt{2}$+5$\sqrt{6}$(m),
答:C、A之间的距离为(15$\sqrt{2}$+5$\sqrt{6}$)m.
点评 此题主要考查了解直角三角形的应用-仰角、俯角问题以及解直角三角形的应用-坡度坡角问题,要求学生借助仰角、坡角关系构造直角三角形,并结合图形利用三角函数求解.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
15. 如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )
如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )
 如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )
如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{5}$ |
 一艘轮船位于灯塔P南偏西60°方向上的点A处,在A正东方向上距离20海里的有一点B处,在灯塔P南偏西45°方向上,求A距离灯塔P的距离.
一艘轮船位于灯塔P南偏西60°方向上的点A处,在A正东方向上距离20海里的有一点B处,在灯塔P南偏西45°方向上,求A距离灯塔P的距离.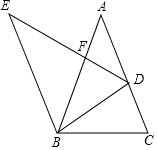 如图△EDB由△ABC绕点B逆时针旋转而来,D点落在AC上,DE交AB于点F,若AB=AC,DB=BF,则AF与BF的比值为$\frac{\sqrt{5}-1}{2}$.
如图△EDB由△ABC绕点B逆时针旋转而来,D点落在AC上,DE交AB于点F,若AB=AC,DB=BF,则AF与BF的比值为$\frac{\sqrt{5}-1}{2}$.