题目内容
4.先化简,再求值:(1+$\frac{1}{{x}^{2}-1}$)÷$\frac{{x}^{2}}{{x}^{2}+2x+1}$,其中x=$\sqrt{2}$+1.分析 首先计算计算括号里面的减法,然后再计算括号外的除法,化简后,再代入x的值,进行计算即可.
解答 解:原式=($\frac{{x}^{2}-1}{{x}^{2}-1}$$\frac{1}{{x}^{2}-1}$)•$\frac{(x+1)^{2}}{{x}^{2}}$,
=$\frac{{x}^{2}}{(x+1)(x-1)}$•$\frac{(x+1)^{2}}{{x}^{2}}$,
=$\frac{x+1}{x-1}$,
当x=$\sqrt{2}$+1时,
原式=$\frac{\sqrt{2}-2}{\sqrt{2}}$=1-$\sqrt{2}$.
点评 此题主要考查了分式的化简求值,在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
15. 如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )
如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )
 如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )
如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{5}$ |
13.△ADE∽△ABC,且相似比为1:3,若△ADE的面积为5,则△ABC的面积为( )
| A. | 10 | B. | 15 | C. | 30 | D. | 45 |
 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6).
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6).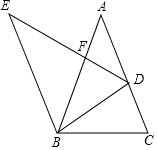 如图△EDB由△ABC绕点B逆时针旋转而来,D点落在AC上,DE交AB于点F,若AB=AC,DB=BF,则AF与BF的比值为$\frac{\sqrt{5}-1}{2}$.
如图△EDB由△ABC绕点B逆时针旋转而来,D点落在AC上,DE交AB于点F,若AB=AC,DB=BF,则AF与BF的比值为$\frac{\sqrt{5}-1}{2}$.