题目内容
3.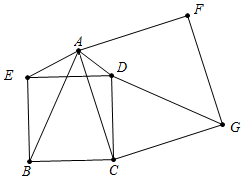 如图,BCDE,ACGF是正方形,三角形AED、CDG的面积分别为4.5与8,那么正方形BCDE的面积是多少?
如图,BCDE,ACGF是正方形,三角形AED、CDG的面积分别为4.5与8,那么正方形BCDE的面积是多少?
分析 如图,作AM⊥BC于M,交DE于N.由△BCA≌△DCG,推出S△ABC=S△DCG=8,推出S△ABC-S△AED=8-4.5=3.5,可得$\frac{1}{2}$•BC•AM-$\frac{1}{2}$DE•AN=3.5,即BC(AM-AN)=7,即BC•MN=7,易证MN=BE,可得S正方形BCDE=BC•BE=7.
解答 解:如图,作AM⊥BC于M,交DE于N.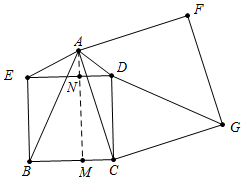
∵四边形BCDE,四边形ACGF都是正方形,
∴BC=CD,CA=CG,∠BCD=∠ACG=90°,
∴∠BCA=∠DCG,
∴△BCA≌△DCG,
∴S△ABC=S△DCG=8,
∴S△ABC-S△AED=8-4.5=3.5,
∴$\frac{1}{2}$•BC•AM-$\frac{1}{2}$DE•AN=3.5,
∴BC(AM-AN)=7,
∴BC•MN=7,易证MN=BE,
∴S正方形BCDE=BC•BE=7.
点评 本题考查正方形的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
15. 如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )
如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )
 如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )
如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{5}$ |
13.△ADE∽△ABC,且相似比为1:3,若△ADE的面积为5,则△ABC的面积为( )
| A. | 10 | B. | 15 | C. | 30 | D. | 45 |
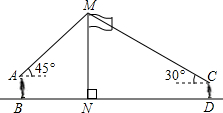 如图,某数学兴趣小组在活动课上测量学校旗杆高度,已知小明的眼睛与地面的距离AB是1.7m,看旗杆顶部M的仰角为45°,小红的眼睛与地面的距离CD是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.【参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,结果保留整数】
如图,某数学兴趣小组在活动课上测量学校旗杆高度,已知小明的眼睛与地面的距离AB是1.7m,看旗杆顶部M的仰角为45°,小红的眼睛与地面的距离CD是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.【参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,结果保留整数】
 如图,为了测量山顶铁塔AE的高,小明在25m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为58m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
如图,为了测量山顶铁塔AE的高,小明在25m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为58m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75) 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6).
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6).