题目内容
5．解不等式组：$\left\{\begin{array}{l}{2x-1＞x+1}\\{3（x-2）-x≤4}\end{array}\right.$，并求出它的所有整数解的和．分析 求出每个不等式的解集，再确定其公共解，得到不等式组的正整数解，求其和即可．
解答 解：$\left\{\begin{array}{l}{2x-1＞x+1①}\\{3（x-2）-x≤4②}\end{array}\right.$，
解不等式①得x＞2，
解不等式②得x≤5，
∴原不等式组的解集是2＜x≤5，
∴原不等式组的整数解是3，4，5，
∴所有整数解的和3+4+5=12．
点评 本题主要考查了一元一次不等式组的解法，并会根据未知数的范围确定它所满足的特殊条件的值．一般方法是先解不等式组，再根据解集求出特殊值．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
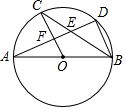如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD；②CB平分∠ABD；③∠AOC=∠AEC；④AF=DF；⑤△CEF≌△BED；⑥BD=2OF．其中一定成立的是（请填序号）①②④⑥．
16．已知点A（x1，y1），B（x2，y2）是反比例函数y=$\frac{1}{x}$图象上的点，若x1＞0＞x2，则一定成立的是（ ）
| A． | y1＞y2＞0 | B． | y1＞0＞y2 | C． | 0＞y1＞y2 | D． | y2＞0＞y1 |
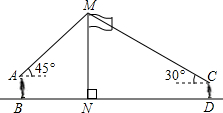如图，某数学兴趣小组在活动课上测量学校旗杆高度，已知小明的眼睛与地面的距离AB是1.7m，看旗杆顶部M的仰角为45°，小红的眼睛与地面的距离CD是1.5m，看旗杆顶部M的仰角为30°．两人相距23m且位于旗杆两侧（点B，N，D在同一条直线上）．请求出旗杆MN的高度．【参考数据：$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7，结果保留整数】
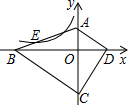如图，四边形ABCD的顶点都在坐标轴上，若AD∥BC，△ACD与△BCD的面积分别为10和20，若双曲线y=$\frac{k}{x}$恰好经过边AB的四等分点E（BE＜AE），则k的值为-$\frac{5}{2}$．
17．下列运算，正确的是（ ）
| A． | 4a3-a2=3a | B． | a6÷a3=a2 | C． | a2•a3=a5 | D． | （-2a）2=-4a2 |
15．
如图，在矩形ABCD中，AB＜AD，E为AD边上一点，且AE=$\frac{1}{2}$AB，连结BE，将△ABE沿BE翻折，若点A恰好落在CE上点F处，则∠CBF的余弦值为（ ）
如图，在矩形ABCD中，AB＜AD，E为AD边上一点，且AE=$\frac{1}{2}$AB，连结BE，将△ABE沿BE翻折，若点A恰好落在CE上点F处，则∠CBF的余弦值为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{4}{5}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{3}{5}$ |