题目内容
12. 把下面的说理过程补充完整:
把下面的说理过程补充完整:如图,已知:∠AED=∠C,∠3=∠B.试判断∠1与∠2的数量关系,并说明理由.(注:理由中的符号“∵”表示“因为”,“∴”表示“所以”)
解:∠1+∠2=180°.理由如下:
∵∠AED=∠C(已知)
∴DE∥BC.(同位角相等,两直线平行)
∴∠B=∠ADE.(两直线平行,同位角相等)
∵∠3=∠B(已知)
∴∠3=∠ADE.(等量代换)
∴EF∥AB.(内错角相等,两直线平行)
∴∠2+∠ADF=180°.(两直线平行,同旁内角互补)
∵∠1=∠ADF.(对顶角相等)
∴∠1+∠2=180°.(等量代换)
分析 根据利用平行线的性质证明两角互补的步骤,把解题过程补充完整即可.
解答 解:∠1+∠2=180°.理由如下:
∵∠AED=∠C(已知)
∴DE∥BC.(同位角相等,两直线平行)
∴∠B=∠ADE.(两直线平行,同位角相等)
∵∠3=∠B(已知)
∴∠3=∠ADE.(等量代换)
∴EF∥AB.(内错角相等,两直线平行)
∴∠2+∠ADF=180°.(两直线平行,同旁内角互补)
∵∠1=∠ADF.(对顶角相等)
∴∠1+∠2=180°.(等量代换)
故答案为:同位角相等,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补;∠ADF;等量代换.
点评 本题考查了平行线的判定及性质以及对顶角的定义,解题的关键是根据平行线的性质找出同旁内角互补.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找出相等或互补的角是关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
3.函数y=$\frac{x+3}{\sqrt{x-2}}$中,自变量x的取值范围是( )
| A. | x>2 | B. | x≥-3 | C. | x>-3 | D. | x≥2 |
1.线段CD是由线段AB平移得到的,点A(-2,5)的对应点为C(3,7),则点B(-4,-7)的对应点D的坐标为( )
| A. | (2,9) | B. | (5,2) | C. | (1,-5) | D. | (-9,-5) |
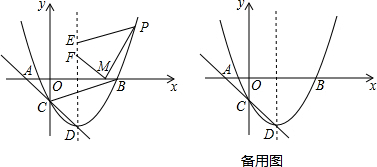
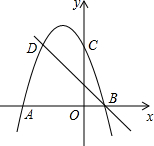 如图,二次函数的图象与x轴交于点A(-3,0),B(1,0),交y轴于点C(0,3),点C,D是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点B,D.
如图,二次函数的图象与x轴交于点A(-3,0),B(1,0),交y轴于点C(0,3),点C,D是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点B,D. 如图,在平行四边形ABCD中,点E、F分别在AB、AD上,且AE=$\frac{1}{3}$AB,AF=$\frac{1}{4}$AD,连结EF交对角线AC于G,则$\frac{AG}{AC}$=$\frac{1}{7}$.
如图,在平行四边形ABCD中,点E、F分别在AB、AD上,且AE=$\frac{1}{3}$AB,AF=$\frac{1}{4}$AD,连结EF交对角线AC于G,则$\frac{AG}{AC}$=$\frac{1}{7}$. 如图,已知二次函数y=x2+bx+c的图象经过点A(-1,0),B(1,-2),该图象与x轴的另一个交点为C,则AC的长为3.
如图,已知二次函数y=x2+bx+c的图象经过点A(-1,0),B(1,-2),该图象与x轴的另一个交点为C,则AC的长为3.