题目内容
2.已知二次函数y=x2+mx+m-5(m是常数).(1)求证:不论m为何值,该函数的图象与x轴一定有两公共点;
(2)若该二次函数的图象过点(0,-3),则将函数图象沿x轴怎样平移能使抛物线过原点?
分析 (1)框将函数问题转化为方程问题,然后证明△>0即可;
(2)将点(0,-3)代入可求得m的值,从而得到抛物线的接下来,然后再求得抛物线与x轴的交点坐标,然后可确定出平移的方向和距离.
解答 解:(1)令y=0得关于x的一元二次方程:x2+mx+m-5=0,则△=b2-4ac=m2-4(m-5)=m2-4m+20=(m-2)2+16.
∵不论m为何值,(m-2)2≥0,
∴(m-2)2+16>0.
∴不论m为何值,一元二次方程x2+mx+m-5=0一定有两个不相等的实数根,
∴不论m为何值,该函数的图象与x轴一定有两公共点.
(2)∵函数图象过点(0,-3),
∴m-5=-3,m=2,
∴二次函数表达式为y=x2+2x-3,
∵令y=0得:x2+2x-3=0解得:x1=1,x2=-3.
∴函数的图象与x轴的两个交点为:(1,0)和(-3,0).
∴将函数图象沿x 轴向右平移3个单位或向左平移1个单位就能使抛物线过原点.
点评 本题主要考查的是二次与x轴的交点问题,求得抛物线与x轴的两交点的坐标是解答问题(2)的关键.

练习册系列答案
相关题目
10.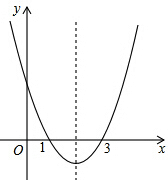 已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )
 已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )| A. | abc<0 | B. | -3a+c<0 | C. | b2-4ac≥0 | D. | 5a+2b+c>0 |
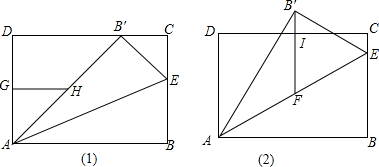
17. 在△ABC中,∠ACB=90°,AC=BC,AB=10,用尺规作图的方法作线段AD和线段DE,保留作图痕迹如图所示,认真观察作图痕迹,则△BDE的周长是( )
在△ABC中,∠ACB=90°,AC=BC,AB=10,用尺规作图的方法作线段AD和线段DE,保留作图痕迹如图所示,认真观察作图痕迹,则△BDE的周长是( )
 在△ABC中,∠ACB=90°,AC=BC,AB=10,用尺规作图的方法作线段AD和线段DE,保留作图痕迹如图所示,认真观察作图痕迹,则△BDE的周长是( )
在△ABC中,∠ACB=90°,AC=BC,AB=10,用尺规作图的方法作线段AD和线段DE,保留作图痕迹如图所示,认真观察作图痕迹,则△BDE的周长是( )| A. | 8 | B. | 5$\sqrt{2}$ | C. | $\frac{15}{2}$$\sqrt{2}$ | D. | 10 |
 如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )
如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )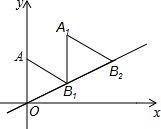 如图放置的△OAB1,△B1A1B2都是边长为2的等边三角形,边AO在y轴上,点B1,B2都在直线y=$\frac{\sqrt{3}}{3}$x上,则点B2的坐标为(2$\sqrt{3}$,2).
如图放置的△OAB1,△B1A1B2都是边长为2的等边三角形,边AO在y轴上,点B1,B2都在直线y=$\frac{\sqrt{3}}{3}$x上,则点B2的坐标为(2$\sqrt{3}$,2).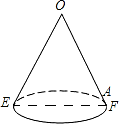 如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.
如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$. 把下面的说理过程补充完整:
把下面的说理过程补充完整: