题目内容
17. 如图,在平行四边形ABCD中,点E、F分别在AB、AD上,且AE=$\frac{1}{3}$AB,AF=$\frac{1}{4}$AD,连结EF交对角线AC于G,则$\frac{AG}{AC}$=$\frac{1}{7}$.
如图,在平行四边形ABCD中,点E、F分别在AB、AD上,且AE=$\frac{1}{3}$AB,AF=$\frac{1}{4}$AD,连结EF交对角线AC于G,则$\frac{AG}{AC}$=$\frac{1}{7}$.
分析 根据题意在AD上截取AH=$\frac{3}{4}$AD,得到AG与OC的关系,然后由相似三角形得到OC与AO的关系,代入求出比值即可.
解答 解:如图,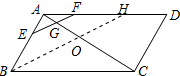 在AD上取点H,使AH=$\frac{3}{4}$AD,连接BH交AC于O,
在AD上取点H,使AH=$\frac{3}{4}$AD,连接BH交AC于O,
则$\frac{AG}{AO}$=$\frac{1}{3}$,即AG=$\frac{1}{3}$AO,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△AOH∽△COB,
∴$\frac{AO}{CO}$=$\frac{AH}{CB}$=$\frac{3}{4}$,
∴CO=$\frac{4}{3}$AO,
∴$\frac{AG}{AC}$=$\frac{AG}{AO+CO}$=$\frac{\frac{1}{3}AO}{AO+\frac{4}{3}AO}$=$\frac{1}{7}$.
故答案为:$\frac{1}{7}$.
点评 本题考查的是相似三角形的判定与性质;通过作辅助线证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
7. 如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )
如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )
 如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )
如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.关于反比例函数y=$\frac{2}{x}$的图象,下列说法正确的是( )
| A. | 图象经过点(1,1) | |
| B. | 当x<0时,y随x的增大而减小 | |
| C. | 图象的两个分支关于x轴成轴对称 | |
| D. | 图象的两个分支分布在第二、四象限 |
9.直线y1=2x+2关于x轴对称的直线为y2,则当y1>y2时,自变量x的取值范围是( )
| A. | x>-1 | B. | x<-1 | C. | x>2 | D. | x>0 |
6.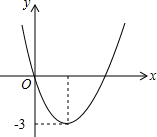 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )
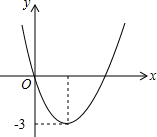 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )| A. | -3 | B. | 3 | C. | -6 | D. | 9 |
 把下面的说理过程补充完整:
把下面的说理过程补充完整: