题目内容
2.解下列方程组和不等式组.(1)$\left\{\begin{array}{l}{\frac{m}{3}+\frac{n}{6}=2}\\{\frac{m}{4}+\frac{n}{4}=2}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3x+1<x-3}\\{\frac{1+x}{2}≤\frac{1+2x}{3}+1}\end{array}\right.$,把解集在数轴上表示出来,并写出它的所有整数解.
分析 (1)原方程组应先化简,然后由于n的系数相同,可考虑用减法消去n,然后求解.
(2)先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.
解答 解:(1)化简为:$\left\{\begin{array}{l}{2m+n=12①}\\{m+n=8②}\end{array}\right.$,
①-②得:m=4,
代入②得:n=4
故方程组的解为:$\left\{\begin{array}{l}{m=4}\\{n=4}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{3x+1<x-3①}\\{\frac{1+x}{2}≤\frac{1+2x}{3}+1②}\end{array}\right.$,
解①得x<-2
解②得:x≥-5,
故不等式组的解集为-5≤x<-2,
在数轴上表示为:
它的所有整数解为-5,-4,-3.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.同时考查了解一元一次不等式组和在数轴上表示不等式的解集.

练习册系列答案
相关题目
 把下面的说理过程补充完整:
把下面的说理过程补充完整: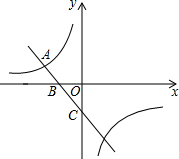 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x-1的图象的一个交点为A(-2,a).
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x-1的图象的一个交点为A(-2,a). 如图,已知AD∥BC,∠C=38°,∠ADB:∠BDC=1:3,则∠ADB=35.5°.
如图,已知AD∥BC,∠C=38°,∠ADB:∠BDC=1:3,则∠ADB=35.5°.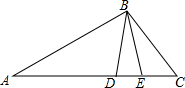 如图,在△ABC中,D是AC上一点,AB2=AD•AC,∠CBD的平分线交AC于点E.求证:AB=AE.
如图,在△ABC中,D是AC上一点,AB2=AD•AC,∠CBD的平分线交AC于点E.求证:AB=AE.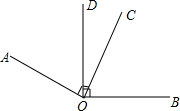 如图,若AO⊥OC,BO⊥DO,
如图,若AO⊥OC,BO⊥DO,