题目内容
4. 如图,已知二次函数y=x2+bx+c的图象经过点A(-1,0),B(1,-2),该图象与x轴的另一个交点为C,则AC的长为3.
如图,已知二次函数y=x2+bx+c的图象经过点A(-1,0),B(1,-2),该图象与x轴的另一个交点为C,则AC的长为3.
分析 把A、B的坐标代入函数解析式,求出b、c的值,得出函数解析式,求出函数与x轴的交点,即可得出答案.
解答 解:∵二次函数y=x2+bx+c的图象经过点A(-1,0),B(1,-2),
∴代入得:$\left\{\begin{array}{l}{1-b+c=0}\\{1+b+c=-2}\end{array}\right.$,
解得:b=-1,c=-2,
即y=x2-x-2,
当y=0时,x2-x-2=0,
解得:x1=2,x2=-1,
∴OA=1,OC=2,
∵AC=3,
故答案为:3.
点评 本题考查了抛物线与x轴的交点,用待定系数法求出函数的解析式的应用,能求出函数与x的轴的交点是解此题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
9.直线y1=2x+2关于x轴对称的直线为y2,则当y1>y2时,自变量x的取值范围是( )
| A. | x>-1 | B. | x<-1 | C. | x>2 | D. | x>0 |
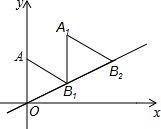 如图放置的△OAB1,△B1A1B2都是边长为2的等边三角形,边AO在y轴上,点B1,B2都在直线y=$\frac{\sqrt{3}}{3}$x上,则点B2的坐标为(2$\sqrt{3}$,2).
如图放置的△OAB1,△B1A1B2都是边长为2的等边三角形,边AO在y轴上,点B1,B2都在直线y=$\frac{\sqrt{3}}{3}$x上,则点B2的坐标为(2$\sqrt{3}$,2). 把下面的说理过程补充完整:
把下面的说理过程补充完整: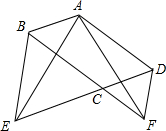 如图,在平行四边形ABCD中,∠BCD=120°,分别延长DC、BC到点E、F,使得△BCE和△CDF都是正三角形.求证:AE=AF.
如图,在平行四边形ABCD中,∠BCD=120°,分别延长DC、BC到点E、F,使得△BCE和△CDF都是正三角形.求证:AE=AF. 如图,已知A(-4,n),B(-1,2)是一次函数y=kx+b与反比例函数$y=\frac{m}{x}$(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
如图,已知A(-4,n),B(-1,2)是一次函数y=kx+b与反比例函数$y=\frac{m}{x}$(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.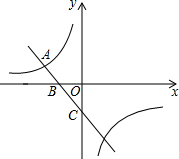 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x-1的图象的一个交点为A(-2,a).
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x-1的图象的一个交点为A(-2,a).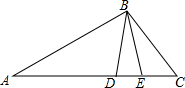 如图,在△ABC中,D是AC上一点,AB2=AD•AC,∠CBD的平分线交AC于点E.求证:AB=AE.
如图,在△ABC中,D是AC上一点,AB2=AD•AC,∠CBD的平分线交AC于点E.求证:AB=AE.