题目内容
1．在以下三个整式中，任取其中的两个进行和或差的运算，使得计算后所得的多项式分别满足相应的要求并解答：x4-2x2y2-y4、x4+y4、2x2y2．（1）该多项式因式分解时，只运用了平方差公式；
（2）该多项式因式分解时，只运用了完全平方公式；
（3）该多项式因式分解时，既运用了平方差公式，又运用了完全平分公式．
分析 （1）直接利用x4-2x2y2-y4与2x2y2相加，进而分解因式即可；
（2）直接利用x4+y4与2x2y2相加，进而分解因式即可；
（3）直接利用x4+y4与2x2y2相减，进而分解因式即可．
解答 解：（1）x4-2x2y2-y4+2x2y2
=x4-y4
=（x2+y2）（x+y）（x-y）；
（2）x4+y4+2x2y2=（x2+y2）2；
（3）x4+y4-2x2y2=（x2-y2）2=（x+y）2（x-y）2．
点评 此题主要考查了公式法分解因式，正确应用乘法公式是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
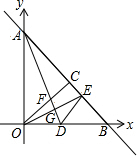如图，在平面直角坐标系中，直线AB与坐标轴分别交于A、B两点，已知点A的坐标为（0，8），点B的坐标为（8，0），OC、AD均是△OAB的中线，OC、AD相交于点F，OE⊥AD于G交AB于E．
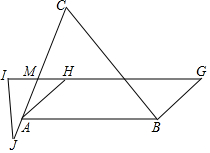如图所示，已知H为△ABC的垂心，点G满足四边形ABGH为平行四边形．I为直线GH上的点，AC交GI于M．且IM=MH．J为CA延长线上一点，且IJ=AH，求证：I、J、G、C四点共圆．（坐标法不得分）