题目内容
5.在平面直角坐标系xOy中,抛物线C:y=mx2+4x+1.(1)当抛物线C经过点A(-5,6)时,求抛物线的表达式及顶点坐标;
(2)若抛物线C:y=mx2+4x+1(m>0)与x轴的交点的横坐标都在-1和0之间(不包括-1和0),结合函数的图象,求m的取值范围;
(3)参考(2)小问思考问题的方法解决以下问题:
关于x的方程x-4=$\frac{a-3}{x}$在0<x<4范围内有两个解,求a的取值范围.
分析 (1)把点A(-5,6)代入抛物线y=mx2+4x+1求出m的值,即可得出抛物线的表达式与顶点坐标;
(2)根据抛物线C:y=mx2+4x+1(m>0)与x轴的交点的横坐标都在-1和0之间可知当x=-1时,y>0,且△≥0,求出m的取值范围即可;
(3)方程x-4=$\frac{a-3}{x}$在0<x<4范围内有两个解即抛物线y=x2-4x-a+3与x轴在0<x<4范围内有两个交点,从而可得当x=0时y>0,x=4时y>0,且△>0,解之可得.
解答 解:(1)∵抛物线C:y=mx2+4x+1经过点A(-5,6),
∴6=25m-20+1,解得m=1,
∴抛物线的表达式为y=x2+4x+1=(x+2)2-3,
∴抛物线的顶点坐标为(-2,-3);
(2)∵抛物线C:y=mx2+4x+1(m>0)与x轴的交点的横坐标都在-1和0之间,
∴当x=-1时,y>0,且△≥0,即 $\left\{\begin{array}{l}{m-4+1>0}\\{16-4m≥0}\end{array}\right.$,
解得:3<m≤4;
(3)方程x-4=$\frac{a-3}{x}$的解即为方程x2-4x-a+3=0的解,
而方程x2-4x-a+3=0的解即抛物线y=x2-4x-a+3与x轴交点的横坐标,
∵方程在0<x<4范围内有两个解,
∴当x=0时y>0,x=4时y>0,且△>0,
即$\left\{\begin{array}{l}{-a+3>0}\\{16-4(-a+3)>0}\end{array}\right.$,
解得:-1<a<3.
点评 本题考查的是抛物线与x轴的交点,熟知抛物线与x轴的交点与一元二次方程根的关系是解答此题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
15.下列各题中,合并同类项结果正确的是( )
| A. | 2m2n-2mn2=0 | B. | 2a2+3a2=6a2 | C. | 4xy-3xy=1 | D. | 2a2+3a2=5a2 |
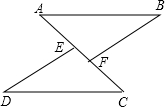 如图,在△ABF与△CDE中,AB=CD,BF=DE,点A、E、F、C在同一条直线上,AE=CF,求证:AB∥CD.
如图,在△ABF与△CDE中,AB=CD,BF=DE,点A、E、F、C在同一条直线上,AE=CF,求证:AB∥CD. 如图,已知:AB⊥DB于点B,CD⊥DB于点D,AB=12,CD=8,BD=28.在DB上是否存在P点,使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似?如果存在,计算出点P的位置;如果不存在,请说明理由.
如图,已知:AB⊥DB于点B,CD⊥DB于点D,AB=12,CD=8,BD=28.在DB上是否存在P点,使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似?如果存在,计算出点P的位置;如果不存在,请说明理由.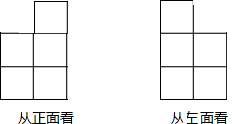 用小立方块搭一个几何体,使得从它的正面和左面看到的形状如图所示.
用小立方块搭一个几何体,使得从它的正面和左面看到的形状如图所示.