题目内容
17. 如图,已知:AB⊥DB于点B,CD⊥DB于点D,AB=12,CD=8,BD=28.在DB上是否存在P点,使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似?如果存在,计算出点P的位置;如果不存在,请说明理由.
如图,已知:AB⊥DB于点B,CD⊥DB于点D,AB=12,CD=8,BD=28.在DB上是否存在P点,使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似?如果存在,计算出点P的位置;如果不存在,请说明理由.
分析 设DP=x,则BP=BD-x=28-x,再分△ABP∽△CDP,△ABP∽△PDC两种情况进行讨论即可.
解答  解:存在.
解:存在.
设DP=x,则BP=BD-x=28-x,
当△ABP∽△CDP时,$\frac{AB}{CD}$=$\frac{BP}{DP}$,即$\frac{12}{8}$=$\frac{28-x}{x}$,解得x=11.2;
当△ABP∽△PDC时,$\frac{AB}{PD}$=$\frac{BP}{DC}$,即$\frac{12}{x}$=$\frac{28-x}{8}$,整理得,x2-28x+96=0,解得x1=4,x2=24,
综上所述,点P在距点D11.2,4或24处.
点评 本题考查了相似三角形的判定,在解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
8.下列各对数中,互为相反数的是( )
| A. | -(-3)和-|-3| | B. | |-2|和|2| | C. | -(-1)和|-1| | D. | |m|与|-m| |
12.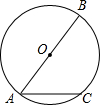 如图,AB是⊙O的直径,AC为⊙O的弦,点D是直径AB上的一点,若OA=5cm,AC=8cm,则CD的长度不可能是( )
如图,AB是⊙O的直径,AC为⊙O的弦,点D是直径AB上的一点,若OA=5cm,AC=8cm,则CD的长度不可能是( )
 如图,AB是⊙O的直径,AC为⊙O的弦,点D是直径AB上的一点,若OA=5cm,AC=8cm,则CD的长度不可能是( )
如图,AB是⊙O的直径,AC为⊙O的弦,点D是直径AB上的一点,若OA=5cm,AC=8cm,则CD的长度不可能是( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 8cm |
7.⊙O的直径为10,圆心O到弦AB的距离为3,则弦AB的长是( )
| A. | 4 | B. | 6 | C. | 7 | D. | 8 |
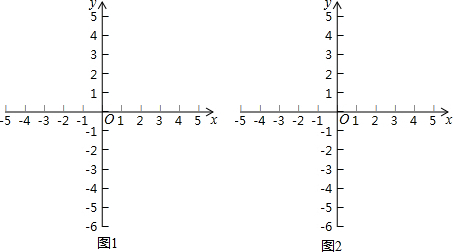
 △ABC三个顶点A、B、C在平面直角坐标系中位置如图所示.将△ABC绕C点顺时针旋转90°,画出旋转后的△A1B1C,并写出A1、B1的坐标.
△ABC三个顶点A、B、C在平面直角坐标系中位置如图所示.将△ABC绕C点顺时针旋转90°,画出旋转后的△A1B1C,并写出A1、B1的坐标.