题目内容
12.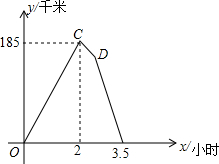 如图所示的图象反映的过程是:甲乙两人同时从A地出发,以各自的速度匀速向B地行驶,甲先到B地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为60km/h,y(km)表示甲乙两人相距的距离,x(h)表示乙行驶的时间.现有以下4个结论:①A、B两地相距305km; ②点D的坐标为(2.5,155); ③甲去时的速度为152.5km/h; ④甲返回的速度是95km/h.以上4个结论中正确的是①②③④.
如图所示的图象反映的过程是:甲乙两人同时从A地出发,以各自的速度匀速向B地行驶,甲先到B地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为60km/h,y(km)表示甲乙两人相距的距离,x(h)表示乙行驶的时间.现有以下4个结论:①A、B两地相距305km; ②点D的坐标为(2.5,155); ③甲去时的速度为152.5km/h; ④甲返回的速度是95km/h.以上4个结论中正确的是①②③④.
分析 首先根据题意解方程得出甲车去时的速度,然后根据题意求得A、B两地的距离即可判断①③的正误;根据两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数关系及乙车的速度为每小时60千米可得出D的坐标即可判断②的正误;根据题意列出方程,通过解方程得出甲车返回的速度即可判断④的正误.
解答 解:
设甲去时的速度为xkm/h,根据题意得
2(x-60)=185,
解得:x=152.5,
由于152.5×2=305,
故A、B两地相距305千米;所以选项①③正确;
∵甲车先到达B地,停留半小时后按原路以另一速度匀速返回,
∴D的横轴应为2.5;
∵乙车的速度为每小时60千米,
∴半小时后行驶距离为30km,故纵轴应为185-30=155;
∴点D的坐标(2.5,155);所以选项②正确;
∵甲车去时的速度为152千米/时;设甲车返回时行驶速度v千米/时,
∴(v+60)×1=155,
解得v=95.
故甲返回的速度是95千米/时.所以选项④正确,
故答案为:①②③④.
点评 本题主要考查了一次函数的综合题,解答要注意数形结合思想的运用,是各地中考的热点,同学们要加强训练,属于中档题.

练习册系列答案
相关题目
3.若x>y,则下列各式变形正确的是( )
| A. | x-6<y-6 | B. | $\frac{x}{2}$<$\frac{y}{2}$ | C. | 2x+1>2y+1 | D. | -x>-y |
7.反比例函数y=$\frac{k}{x}$,若k<0,则( )
| A. | y的值为负 | |
| B. | 双曲线在一、三象限 | |
| C. | y随x的增大而增大 | |
| D. | 在所在的每一个象限,y随x的增大而增大 |
17.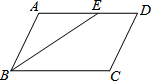 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )| A. | 12 | B. | 18 | C. | 24 | D. | 32 |
4.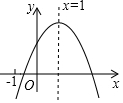 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;
②b>a+c;③9a+3b+c>0; ④c<-3a; ⑤a+b≥m(am+b),其中正确的有( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b>a+c;③9a+3b+c>0; ④c<-3a; ⑤a+b≥m(am+b),其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
1. 如图,D是AB上一点,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED的度数为( )
如图,D是AB上一点,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED的度数为( )
 如图,D是AB上一点,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED的度数为( )
如图,D是AB上一点,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED的度数为( )| A. | 38° | B. | 48° | C. | 52° | D. | 62° |
2.若a>b,则下列式子正确的是( )
| A. | -2a>-2b | B. | $\frac{a}{2}$<$\frac{b}{2}$ | C. | 4-a<4-b | D. | a-4<b-4 |