题目内容
4. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;
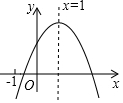
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b>a+c;③9a+3b+c>0; ④c<-3a; ⑤a+b≥m(am+b),其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据抛物线的开口方向、x=-1、x=3时的函数值小于0、对称轴x=-$\frac{b}{2a}$=1及函数的最大值逐一判断可得.
解答 解:∵抛物线开口向下,
∴a<0,
∵-$\frac{b}{2a}$>0,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,
∴结论①错误;
∵当x=-1时,y=a-b+c<0,即b>a+c,
∴结论②正确;
∵当x=-1和x=3时,函数值相等,均小于0,
∴y=9a+3b+c<0,
∴结论③错误;
∵x=-$\frac{b}{2a}$=1,
∴b=-2a,
由x=-1时,y=a-b+c<0得a+2a+c<0,即c<-3a,
∴④正确;
由图象知当x=1时函数取得最大值,
∴am2+bm+c≤a+b+c,即a+b≥m(am+b),
故⑤正确;
故选:B.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列调查,适合用普查方式的是( )
| A. | 调查全市初中学生的每天课外阅读时间 | |
| B. | 调查全市学生每天的睡眠时间 | |
| C. | 调查全市初中学生的视力情况 | |
| D. | 调查一个班级学生的身高 |
9.在平面直角坐标系中,点A在第一象限,点B在x轴正半轴上,∠AOB=60°,OA=8.点A的坐标是( )
| A. | (4,8) | B. | (4,4 $\sqrt{3}$) | C. | (4$\sqrt{3}$,4) | D. | (8,4) |
16.已知两圆的半径分别为1和5,圆心距为4,那么两圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
13. 如图,点A.B.C在⊙D上,∠ABC=70°,则∠ADC的度数为( )
如图,点A.B.C在⊙D上,∠ABC=70°,则∠ADC的度数为( )
 如图,点A.B.C在⊙D上,∠ABC=70°,则∠ADC的度数为( )
如图,点A.B.C在⊙D上,∠ABC=70°,则∠ADC的度数为( )| A. | 110° | B. | 140° | C. | 35° | D. | 130° |
14.甲、乙两人练习跑步,若乙先跑10米,则甲跑5秒就能追上乙,若乙先跑2秒,则甲跑4秒就可追上乙.设甲,乙每秒分别跑x米,y米,则下列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{5(x-y)=10}\\{4(x-y)=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x-5y=-10}\\{4x-4y=2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x-5y=10}\\{4x-4y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{5x-5y=10}\\{4x=6y}\end{array}\right.$ |
 如图,二次函数的图象与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,-2).
如图,二次函数的图象与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,-2).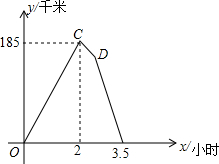 如图所示的图象反映的过程是:甲乙两人同时从A地出发,以各自的速度匀速向B地行驶,甲先到B地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为60km/h,y(km)表示甲乙两人相距的距离,x(h)表示乙行驶的时间.现有以下4个结论:①A、B两地相距305km; ②点D的坐标为(2.5,155); ③甲去时的速度为152.5km/h; ④甲返回的速度是95km/h.以上4个结论中正确的是①②③④.
如图所示的图象反映的过程是:甲乙两人同时从A地出发,以各自的速度匀速向B地行驶,甲先到B地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为60km/h,y(km)表示甲乙两人相距的距离,x(h)表示乙行驶的时间.现有以下4个结论:①A、B两地相距305km; ②点D的坐标为(2.5,155); ③甲去时的速度为152.5km/h; ④甲返回的速度是95km/h.以上4个结论中正确的是①②③④.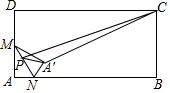 如图,在矩形ABCD中,AB=4,AD=2,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A'MN,连接A'C.在MN上存在一动点P.连接A'P、CP,则△A'PC周长的最小值是$\sqrt{17}$-1+2$\sqrt{5}$.
如图,在矩形ABCD中,AB=4,AD=2,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A'MN,连接A'C.在MN上存在一动点P.连接A'P、CP,则△A'PC周长的最小值是$\sqrt{17}$-1+2$\sqrt{5}$.