题目内容
20.如图1,△ABC和△CDE为等边三角形,且边长分别为a,b,点D和E分别在边AC和BC上,点F,G,H,I分别为AB,BE,ED,AD的中点,连接FG,GH,HI,IF(1)判断四边形FGHI是什么特殊四边形?并说明理由.
(2)当a=6,b=2时,求四边形FGHI的周长.
(3)如图2,当四边形FGHI是正方形时,连接AE,BD,相交于点N,点N,H恰好在FC上,若a=2+$\sqrt{3}$,求b的值.

分析 (1)根据△ABC和△CDE为等边三角形,可得四边形ABED是等腰梯形,再根据点F,G,H,I分别为AB,BE,ED,AD的中点,即可得出FG=IH=FI=GH,进而得到四边形FGHI是菱形;
(2)过A作AM⊥BC于M,连接AE,再根据勾股定理,求得Rt△ACM中,AM=3$\sqrt{3}$,Rt△AEM中,AE=2$\sqrt{7}$,由(1)可得,四边形FGHI是菱形,且AE=2FG,即可得出四边形FGHI的周长=4FG=2AE;
(3)连接GI,根据四边形ABED是等腰梯形,G,I分别为BE,AD的中点,即可得到GI=$\frac{1}{2}$(2+$\sqrt{3}$+b),再根据四边形FGHI是正方形,可得FH=GI=$\frac{1}{2}$(2+$\sqrt{3}$+b),再根据△ABC和△CDE为等边三角形,F、H分别是AB、DE的中点,运用三线合一得出CF⊥AB,CH⊥DE,最后根据DE∥AB,得到$\frac{CH}{CF}$=$\frac{DE}{AB}$,列出关于b的方程式进行求解即可.
解答 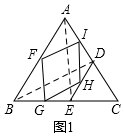 解:(1)四边形FGHI是菱形.
解:(1)四边形FGHI是菱形.
如图1,连接AE,BD,
∵△ABC和△CDE为等边三角形,
∴DE∥AB,AD=BE,
∴四边形ABED是等腰梯形,
∴AE=BD,
又∵点F,G,H,I分别为AB,BE,ED,AD的中点,
∴FG=IH=$\frac{1}{2}$AE,FI=GH=$\frac{1}{2}$BD,
∴FG=IH=FI=GH,
∴四边形FGHI是菱形;
(2)当a=6,b=2时,BC=AC=6,CE=2,
如图,过A作AM⊥BC于M,连接AE,
∵△ABC是等边三角形,
∴CM=$\frac{1}{2}$BC=3,ME=3-2=1,
又∵Rt△ACM中,AM=$\sqrt{A{C}^{2}-C{M}^{2}}$=3$\sqrt{3}$,
∴Rt△AEM中,AE=$\sqrt{A{M}^{2}+M{E}^{2}}$=2$\sqrt{7}$,
由(1)可得,四边形FGHI是菱形,且AE=2FG,
∴四边形FGHI的周长=4FG=2AE=4$\sqrt{7}$;
(3)如图2,连接GI,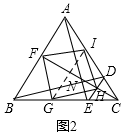
∵四边形ABED是等腰梯形,G,I分别为BE,AD的中点,
∴GI=$\frac{1}{2}$(DE+AB)=$\frac{1}{2}$(2+$\sqrt{3}$+b),
∵四边形FGHI是正方形,
∴FH=GI=$\frac{1}{2}$(2+$\sqrt{3}$+b),
∵△ABC和△CDE为等边三角形,F、H分别是AB、DE的中点,
∴CF⊥AB,CH⊥DE,
∴Rt△CDH中,CH=$\sqrt{3}$DH=$\frac{\sqrt{3}}{2}$b,
又∵DE∥AB,
∴△CDE∽△CAB,
∴$\frac{CH}{CF}$=$\frac{DE}{AB}$,
即$\frac{\frac{\sqrt{3}}{2}b}{\frac{\sqrt{3}}{2}b+\frac{1}{2}(2+\sqrt{3}+b)}$=$\frac{b}{2+\sqrt{3}}$,
解得b=1,
故b的值为1.
点评 本题属于四边形综合题,主要考查了菱形的判定,正方形的性质,中点四边形,梯形中位线定理,相似三角形的性质以及勾股定理的综合应用,解决问题的关键是依据三角形中位线定理,计算菱形的周长;解题时注意:相似三角形对应高的比等于相似比,据此可得比例式,解方程可得出b的值.

| A. | x≠-3 | B. | x≠3 | C. | x>-3 | D. | x<-3 |
| A. | 调查全市初中学生的每天课外阅读时间 | |
| B. | 调查全市学生每天的睡眠时间 | |
| C. | 调查全市初中学生的视力情况 | |
| D. | 调查一个班级学生的身高 |
| A. | 2x+1 | B. | -2x-1 | C. | 1 | D. | 7 |
| A. | (4,8) | B. | (4,4 $\sqrt{3}$) | C. | (4$\sqrt{3}$,4) | D. | (8,4) |
| A. | -b2+2ab | B. | 25n2+10n | C. | 9-6a+a2 | D. | a2+b2+2a |
 定义:三边长和面积都是整数的三角形称为“整数三角形”.
定义:三边长和面积都是整数的三角形称为“整数三角形”.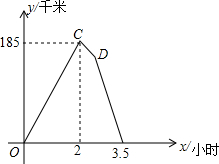 如图所示的图象反映的过程是:甲乙两人同时从A地出发,以各自的速度匀速向B地行驶,甲先到B地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为60km/h,y(km)表示甲乙两人相距的距离,x(h)表示乙行驶的时间.现有以下4个结论:①A、B两地相距305km; ②点D的坐标为(2.5,155); ③甲去时的速度为152.5km/h; ④甲返回的速度是95km/h.以上4个结论中正确的是①②③④.
如图所示的图象反映的过程是:甲乙两人同时从A地出发,以各自的速度匀速向B地行驶,甲先到B地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为60km/h,y(km)表示甲乙两人相距的距离,x(h)表示乙行驶的时间.现有以下4个结论:①A、B两地相距305km; ②点D的坐标为(2.5,155); ③甲去时的速度为152.5km/h; ④甲返回的速度是95km/h.以上4个结论中正确的是①②③④.