题目内容
2.如图(a),在Rt△ABC中,∠C=90°,AC=2,BC=1,现以AB所在直线为对称轴,△ABC经轴对称变换后的图形为△DEF.(1)求四边形ACBF的面积;
(2)如图(b),若△ABC和△DEF从初始位置(如图(a)所示)在射线AB上沿AB方向同时开始平移,△ABC的运动速度是每秒2个单位,△DEF的运动速度是每秒1个单位,设运动时间为t秒.
①当0<t<$\sqrt{5}$时,求线段AE的长度(用含t的代数式表示);
②当△AEF是等腰三角形时,求t的值;
(3)在第(2)题的图形运动过程中,是否存在一点A、C、B、F组成的四边形为矩形?若存在,请直接写出此时t的值;若不存在,请说明理由.
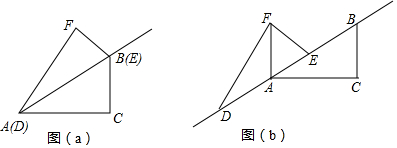
分析 (1)由题意可知:△DEF是由△ABC翻折所得,所以四边形ACBF的面积就是两个△ABC的面积;
(2)①根据AE=DE+A′D-A′A代入可得结果;
②当0<t<$\sqrt{5}$时,分三种情况:任意两边相等时,找一等量关系列方程可得t的值,当t>$\sqrt{5}$时,如图(d),因为∠AEF是钝角,所以△AEF是等腰三角形时只存在一种情况:根据EF=AE列方程可得结论;
(3)当四边形ACBF是矩形时,AF=BC=EF=1,由(2)得:此时t=$\frac{3\sqrt{5}}{5}$.
解答  解:(1)如图(a),由题意得:S四边形ACBF=2S△ABC=2×$\frac{1}{2}$AC×BC=2×1=2;
解:(1)如图(a),由题意得:S四边形ACBF=2S△ABC=2×$\frac{1}{2}$AC×BC=2×1=2;
(2)①由勾股定理得:AB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
设点A的起点为A′,则AE=DE+A′D-A′A=$\sqrt{5}$+t-2t=$\sqrt{5}$-t;
②当0<t<$\sqrt{5}$时,分三种情况:
i)AE=EF时,即$\sqrt{5}$-t=1,
t=$\sqrt{5}$-1;
ii)AE=AF时,
∴∠AFE=∠AEF,
∴∠ADF=∠AFD,
∴AD=AF,
∴$\sqrt{5}$-t=t,
t=$\frac{\sqrt{5}}{2}$;
iii)AF=EF时,如图(c),过F作FG⊥AE于G,则AG=EG,
tan∠FEG=$\frac{FG}{EG}$=$\frac{DF}{EF}$=2,
设FG=2x,EG=x,
由勾股定理得:(2x)2+x2=12,
x=$±\frac{\sqrt{5}}{5}$,
∴AE=2EG=$\frac{2\sqrt{5}}{5}$,
∴$\sqrt{5}$-t=$\frac{2\sqrt{5}}{5}$,
∴t=$\frac{3\sqrt{5}}{5}$,
当t>$\sqrt{5}$时,如图(d),AE=AA′-A′D-DE=2t-t-$\sqrt{5}$=t-$\sqrt{5}$,
当EF=AE时,△AEF是等腰三角形,
即t-$\sqrt{5}$=1,
t=$\sqrt{5}$+1;
综上所述,当△AEF是等腰三角形时,t的值是$\sqrt{5}$-1或$\frac{\sqrt{5}}{2}$或$\frac{3\sqrt{5}}{5}$或$\sqrt{5}$+1;
(3)存在,
如图1,当四边形ACBF是矩形时,
AF=BC=1,
∴AF=EF=1
由(2)得:此时t=$\frac{3\sqrt{5}}{5}$;
∴点A、C、B、F组成的四边形为矩形时,t=$\frac{3\sqrt{5}}{5}$.
点评 本题是四边形综合题,考查了平行四边形的判定、矩形的性质和判定、勾股定理、等腰三角形定义等知识,解题的关键是正确画出图形,学会分类讨论,属于中考压轴题.

| A. | x2-y2 | B. | y2-x2 | C. | -x2-y2 | D. | x2+y2 |
| A. | x≠-3 | B. | x≠3 | C. | x>-3 | D. | x<-3 |
 如图:已知△ABC中,AD是中线,且∠1=∠2,求证:AB=AC.
如图:已知△ABC中,AD是中线,且∠1=∠2,求证:AB=AC. 定义:三边长和面积都是整数的三角形称为“整数三角形”.
定义:三边长和面积都是整数的三角形称为“整数三角形”.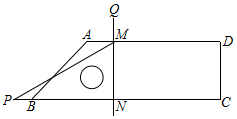 已知四边形ABCD,∠ABC=45°,∠C=∠D=90°,含30°角(∠P=30°)的直角三角板PMN(如图)在图中平移,直角边MN⊥BC,顶点M、N分别在边AD、BC上,延长NM到点Q,使QM=PB.若BC=10,CD=3,则当点M从点A平移到点D的过程中,点Q的运动路径长为7$\sqrt{2}$.
已知四边形ABCD,∠ABC=45°,∠C=∠D=90°,含30°角(∠P=30°)的直角三角板PMN(如图)在图中平移,直角边MN⊥BC,顶点M、N分别在边AD、BC上,延长NM到点Q,使QM=PB.若BC=10,CD=3,则当点M从点A平移到点D的过程中,点Q的运动路径长为7$\sqrt{2}$. 如图,二次函数的图象与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,-2).
如图,二次函数的图象与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,-2).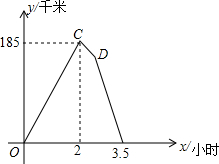 如图所示的图象反映的过程是:甲乙两人同时从A地出发,以各自的速度匀速向B地行驶,甲先到B地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为60km/h,y(km)表示甲乙两人相距的距离,x(h)表示乙行驶的时间.现有以下4个结论:①A、B两地相距305km; ②点D的坐标为(2.5,155); ③甲去时的速度为152.5km/h; ④甲返回的速度是95km/h.以上4个结论中正确的是①②③④.
如图所示的图象反映的过程是:甲乙两人同时从A地出发,以各自的速度匀速向B地行驶,甲先到B地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为60km/h,y(km)表示甲乙两人相距的距离,x(h)表示乙行驶的时间.现有以下4个结论:①A、B两地相距305km; ②点D的坐标为(2.5,155); ③甲去时的速度为152.5km/h; ④甲返回的速度是95km/h.以上4个结论中正确的是①②③④.