题目内容
17.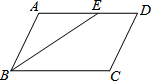 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )| A. | 12 | B. | 18 | C. | 24 | D. | 32 |
分析 由在?ABCD中,∠ABC的平分线交AD于点E,易证得△ABE是等腰三角形,求出AD,继而求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=4,
∴AD=AE+DE=5,
当平行四边形ABCD是矩形时,面积最大=AB•AD=4×6=24;
故选:C.
点评 此题考查了平行四边形的性质以及等腰三角形的判定与性质.注意证得△ABE是等腰三角形是解此题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
5.若-4≤x≤3,化简$\sqrt{{x}^{2}+8x+16}$-$\sqrt{{x}^{2}-6x+9}$的结果为( )
| A. | 2x+1 | B. | -2x-1 | C. | 1 | D. | 7 |
2.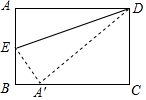 一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( )
一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( )
 一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( )
一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( )| A. | $\frac{5}{3}$cm | B. | $\frac{4}{3}$cm | C. | $\frac{3}{2}$cm | D. | $\frac{7}{5}$cm |
9.在平面直角坐标系中,点A在第一象限,点B在x轴正半轴上,∠AOB=60°,OA=8.点A的坐标是( )
| A. | (4,8) | B. | (4,4 $\sqrt{3}$) | C. | (4$\sqrt{3}$,4) | D. | (8,4) |
6. 如图,两条宽度都是1的纸条,交叉重叠放在一起,且夹角为α,则重叠部分的面积为( )
如图,两条宽度都是1的纸条,交叉重叠放在一起,且夹角为α,则重叠部分的面积为( )
 如图,两条宽度都是1的纸条,交叉重叠放在一起,且夹角为α,则重叠部分的面积为( )
如图,两条宽度都是1的纸条,交叉重叠放在一起,且夹角为α,则重叠部分的面积为( )| A. | $\frac{1}{sinα}$ | B. | $\frac{1}{cosα}$ | C. | tanα | D. | 1 |
7.在Rt△ABC中,∠C=90°,BC=12,AC=16,则斜边AB边上的高CD的长是( )
| A. | 20 | B. | 10 | C. | 9.6 | D. | 8 |
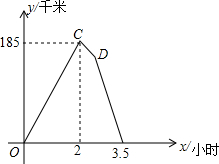 如图所示的图象反映的过程是:甲乙两人同时从A地出发,以各自的速度匀速向B地行驶,甲先到B地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为60km/h,y(km)表示甲乙两人相距的距离,x(h)表示乙行驶的时间.现有以下4个结论:①A、B两地相距305km; ②点D的坐标为(2.5,155); ③甲去时的速度为152.5km/h; ④甲返回的速度是95km/h.以上4个结论中正确的是①②③④.
如图所示的图象反映的过程是:甲乙两人同时从A地出发,以各自的速度匀速向B地行驶,甲先到B地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为60km/h,y(km)表示甲乙两人相距的距离,x(h)表示乙行驶的时间.现有以下4个结论:①A、B两地相距305km; ②点D的坐标为(2.5,155); ③甲去时的速度为152.5km/h; ④甲返回的速度是95km/h.以上4个结论中正确的是①②③④.