题目内容
10. 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的圆交AC于点D,连接OD并延长交BC的延长线于E点,连接AE.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的圆交AC于点D,连接OD并延长交BC的延长线于E点,连接AE.(1)求证:∠BAC=∠DBC;
(2)求证:△EDC~△EBD;
(3)已知:EC•BE=4a2(a>0),tan∠BCD=2,求圆的半径(用含α的式子表示)
分析 (1)直接利用圆周角定理结合互余的性质得出:∠BAC=∠DBC;
(2)利用(1)中所求,结合相似三角形的判定方法得出答案;
(3)利用相似三角形的性质结合锐角三角函数关系得出相似比,进而求出答案.
解答 (1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠BAD+∠ABD=90°,
∵∠ABC=90°,
∴∠ABD+∠DBC=90°,
∴∠BAD=∠DBC;
(2)证明:∵OA=OD,
∴∠BAC=∠ODA,
∵∠BAC=∠DBC,
∴∠ODA=∠DBC,
又∵∠AOD=∠CDE,
∴∠CDE=∠DBE,
又∵∠DEC=∠BED,
∴△EDC~△EBD;
(3)解:∵△EDC~△EBD,
∴$\frac{DE}{EC}$=$\frac{BE}{DE}$,
∴DE2=EC•BE,
∵EC•BE=4a2(a>0),
∴DE=2a,
∵tan∠BCD=$\frac{BD}{DC}$=2,
∴$\frac{DE}{EC}$=$\frac{BE}{DE}$=$\frac{BD}{DC}$=2,
∴DE=4a,EC=a,
∴BC=3a,
又∵tan∠BCD=$\frac{AB}{BC}$=2,
∴AB=6a,
则圆的半径为3a.
点评 此题主要考查了圆的综合以及相似三角形的判定与性质等知识,正确得出△EDC和△EBD的相似比是解题关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
20.下列各数:3.14,$\sqrt{4}$,$\root{3}{9}$,-$\frac{22}{7}$,$\frac{\sqrt{5}}{2}$,π,其中无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.已知实数x,y满足$\sqrt{2x+y-5}$+x2+4y2=4xy,则(x-y)2017的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2016 |
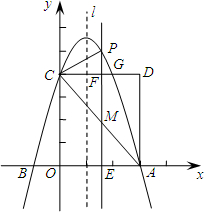 如图所示,在矩形OADC中,以点O为原点,以OA,OC所在直线分别为x轴,y轴建立平面直角坐标系,且抛物线y=-x2+bx+c与x轴交于点A,与y轴交于点C,且D点的坐标为(6,8).
如图所示,在矩形OADC中,以点O为原点,以OA,OC所在直线分别为x轴,y轴建立平面直角坐标系,且抛物线y=-x2+bx+c与x轴交于点A,与y轴交于点C,且D点的坐标为(6,8). 如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=a,DE=b,取c=10,a-b=2.
如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=a,DE=b,取c=10,a-b=2. 如图,网格中每个小正方形的边长都为1,A、B、C都在格点上,试问△ABC是直角三角形吗?请说明理由.
如图,网格中每个小正方形的边长都为1,A、B、C都在格点上,试问△ABC是直角三角形吗?请说明理由.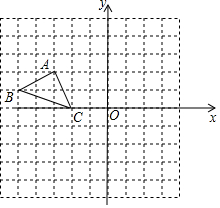 在平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,2).
在平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,2).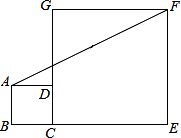 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是$\frac{3\sqrt{5}}{5}$.
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是$\frac{3\sqrt{5}}{5}$.