题目内容
2.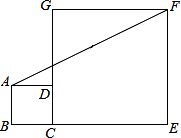 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是$\frac{3\sqrt{5}}{5}$.
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是$\frac{3\sqrt{5}}{5}$.
分析 作CH⊥AF,垂足为H.根据△ADK∽△FGK,求出KF的长,再根据△CHK∽△FGK,求出CH的长.
解答 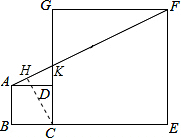 解:作CH⊥AF,垂足为H.
解:作CH⊥AF,垂足为H.
∵CD=BC=1,
∴GD=3-1=2,
∵△ADK∽△FGK,
∴$\frac{DK}{GK}=\frac{AD}{GF}$,
即 $\frac{DK}{GK}$=$\frac{1}{3}$,
∴DK=2×$\frac{1}{4}$=$\frac{1}{2}$,GK=2×$\frac{3}{4}$=$\frac{3}{2}$,
∴KF=$\sqrt{(\frac{3}{2})^{2}+{3}^{2}}$=$\frac{3\sqrt{5}}{2}$,
∵△CHK∽△FGK,
∴$\frac{CH}{GF}=\frac{CK}{FK}$,
∴$\frac{CH}{3}=\frac{1+\frac{1}{2}}{\frac{3\sqrt{5}}{2}}$,
∴CH=$\frac{3\sqrt{5}}{5}$.
故答案为:$\frac{3\sqrt{5}}{5}$.
点评 本题考查了勾股定理,利用勾股定理求出三角形的边长,再构造相似三角形是解题的关键.

练习册系列答案
相关题目
11.已知一次函数y=kx+b的图象经过第二、三、四象限,则反比例函数y=$\frac{kb}{x}$的图象在( )
| A. | 第一、二象限 | B. | 第三、四象限 | C. | 第一、三象限 | D. | 第二、四象限. |
8.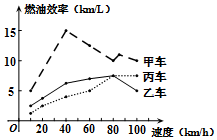 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )| A. | 当行驶速度为40km/h时,每消耗1升汽油,甲车能行驶20km | |
| B. | 消耗1升汽油,丙车最多可行驶5km | |
| C. | 当行驶速度为80km/h时,每消耗1升汽油,乙车和丙车行驶的最大公里数相同 | |
| D. | 当行驶速度为60km/h时,若行驶相同的路程,丙车消耗的汽油最少 |
 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的圆交AC于点D,连接OD并延长交BC的延长线于E点,连接AE.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的圆交AC于点D,连接OD并延长交BC的延长线于E点,连接AE.
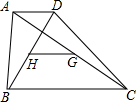 如图,在四边形ABCD中,AD∥BC,AB与CD不平行,H、G分别是两条对角线BD、AC的中点,求证:GH∥AD,且GH=$\frac{1}{2}$(BC-AD).
如图,在四边形ABCD中,AD∥BC,AB与CD不平行,H、G分别是两条对角线BD、AC的中点,求证:GH∥AD,且GH=$\frac{1}{2}$(BC-AD).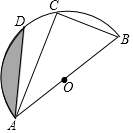 已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为12,且BC=6,∠DAB=45°.(1)求∠DAC的度数;(2)求图中阴影部分的面积(结果保留π).
已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为12,且BC=6,∠DAB=45°.(1)求∠DAC的度数;(2)求图中阴影部分的面积(结果保留π).