题目内容
5. 如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=a,DE=b,取c=10,a-b=2.
如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=a,DE=b,取c=10,a-b=2.(1)正方形EFGH的面积为4,四个直角三角形的面积和为96;
(2)求(a+b)2的值.
分析 (1)由题意可知HE=a-b=2,可求得正方形EFGH的面积,利用四个直角三角形的面积和=正方形ABCD的面积-正方形EFGH的面积,可求得答案;
(2)利用勾股定理可求得a2+b2的值,利用四个直角三角形的面积可求得2ab,则可求得答案.
解答 解:
(1)∵HE=a-b=2,
∴S正方形EFGH=HE2=4,
∵AD=c=10,
∴S正方形ABCD=AD2=100,
∴四个直角三角形的面积和=S正方形ABCD-S正方形EFGH=100-4=96,
故答案为:4;96;
(2)由(1)可知四个直角三角形的面积和为96,
∴4×$\frac{1}{2}$ab=96,解得2ab=96,
∵a2+b2=c2=100,
∴(a+b)2=a2+b2+2ab=100+96=196.
点评 本题主要考查勾股定理的证明及应用,理解图形中四个三角形的面积和等于大正方形的面积与小正方形面积的差是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知A,B,C三点共线,线段AB=25cm,BC=16cm,点E,F分别是线段AB,BC的中点,则线段EF的长为( )
| A. | 21cm或4cm | B. | 20.5cm | C. | 4.5cm | D. | 20.5cm或4.5cm |
20.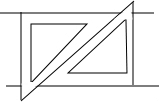 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )
如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )
 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )
如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )| A. | 同位角相等,两直线平行 | B. | 内错角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 平行于同一条直线的两直线平行 |
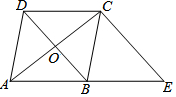 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.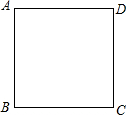 在正方形ABCD中,点E是边BC上的中点,在边CD上取一点F,使得AE平分∠BAF.
在正方形ABCD中,点E是边BC上的中点,在边CD上取一点F,使得AE平分∠BAF. 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的圆交AC于点D,连接OD并延长交BC的延长线于E点,连接AE.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的圆交AC于点D,连接OD并延长交BC的延长线于E点,连接AE.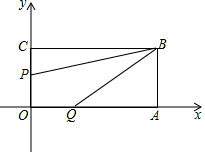 如图长方形OABC的位置如图所示,点B的坐标为(8,4),点P从点C出发向点O移动,速度为每秒1个单位;点Q同时从点O出发向点A移动,速度为每秒2个单位,设运动时间为t(0≤t≤4)
如图长方形OABC的位置如图所示,点B的坐标为(8,4),点P从点C出发向点O移动,速度为每秒1个单位;点Q同时从点O出发向点A移动,速度为每秒2个单位,设运动时间为t(0≤t≤4)