题目内容
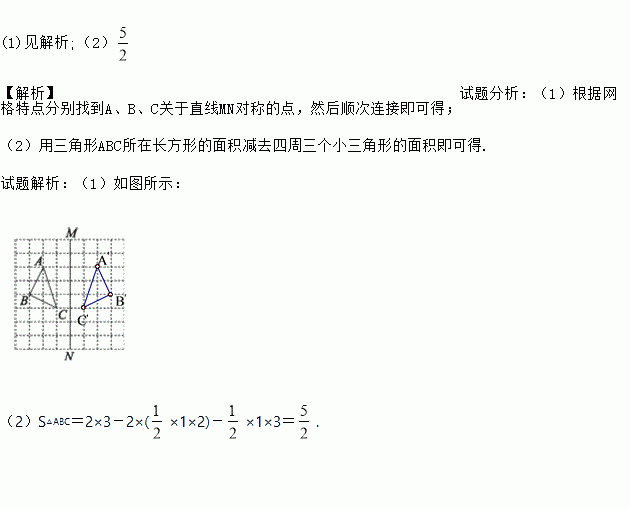
如图，在正方形网格上有一个△ABC.
(1)作△ABC关于直线MN的对称图形(不写作法)；
(2)在网格上的最小正方形的边长为1，求△ABC的面积．
(1)见解析;（2）
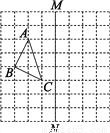
【解析】试题分析：（1）根据网格特点分别找到A、B、C关于直线MN对称的点，然后顺次连接即可得；
（2）用三角形ABC所在长方形的面积减去四周三个小三角形的面积即可得.
试题解析：（1）如图所示：
（2）S△ABC＝2×3－2×(×1×2)－×1×3＝.
练习册系列答案
相关题目
已知a+b=-5,ab=7,求a2+b2的值.
11
【解析】试题分析：根据完全平方公式的变形进行计算即可．
试题解析：【解析】
因为a+b=-5，ab=7，
所以a2+b2=（a+b）2-2ab=（-5）2-2×7=11． 若m＜n，比较下列各式的大小：
（1）m－3______n－3 （2）－5m______－5n （3）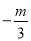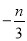
______
（4）3－m______2－n (5)0_____m－n （6）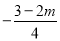
_____
< > > > > <
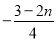
【解析】(1)m如图，△ABC中，AB=AC，AD是∠BAC的平分线．已知AB=5，AD=3，则BC的长为（ ）
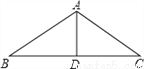
A. 5 B. 6 C. 8 D. 10
C
【解析】因为AB＝AC，AD是∠BAC的平分线，所以BC=2BD.
因为BD＝4，所以BC=2BD=2×4=8.
故选C. 如图，∠AOB＝30°，角内有一点P，PO＝10cm，两边上各有一点Q，R(均不同于点O)，则△PQR的周长的最小值是多少？
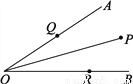
10cm
【解析】试题分析：设点P关于OA的对称点是E，关于OB的对称点是F，当点R、Q在EF上时，△PQR的周长=PQ+QR+PR=EF，此时周长最小．
试题解析：作出点P关于OA的对称点E，作出点P关于OB的对称点F，连接EF，交OA于Q，交OB于R．连接PQ，PR，PE，PF，OE，OF，
则PQ=EQ，PR=RF，
则△PQR的周长=PQ+QR+PR=EQ+QR+R... 如图，BC＝32cm，DE是AB的垂直平分线，D是垂足，DE交BC于E，AC＝18cm，则△AEC的周长为___cm.
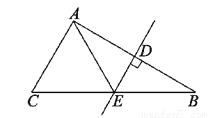
50
【解析】∵DE是AB的垂直平分线，
∴AE=BE．
∴△AEC的周长=AC+CE+AE=AC+BC=18+32=50（cm），
故答案为：50． 如图，已知△ABC中，AC+BC=24，AO，BO分别是角平分线，且MN∥BA，分别交AC于N，BC于M，则△CMN的周长为（ ）
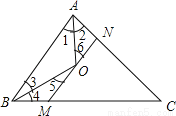
A.12 B.24 C.36 D.不确定
B
【解析】
试题分析：由AO，BO分别是角平分线求得∠1=∠2，∠3=∠4，利用平行线性质求得，∠1=∠6，∠3=∠5，利用等量代换求得∠2=∠6，∠4=∠5，即可解题．
【解析】
由AO，BO分别是角平分线得∠1=∠2，∠3=∠4，
又∵MN∥BA，∴∠1=∠6，∠3=∠5，
∴∠2=∠6，∠4=∠5，
∴AN=NO，BM=OM．
∵AC+BC=24... 如图，在△ABC中，已知∠C＝90°，AC=4，BC=3，那么下列结论不正确的是（ ）
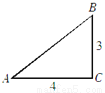
A. sinA=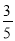
B. cosA=
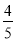C. tanA=
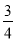D. cosB=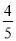
D
【解析】∵∠C＝90°，AC=4，BC=3，∴AB==5，
∴sinA==，cosA== ， tanA== ， cosB==，
故选D. 分解因式：6x－4xy
2x(3－2y)
【解析】试题分析：根据提公因式法分解因式，先确定公因式2x，再提取公因式即可.
试题解析：6x-4xy=2x（3-2y）.