题目内容
下列数值中，是不等式x－2＞2的一个解的是( )
A. 0 B. 2
C. 4 D. 6
D
【解析】解不等式x?2>2，得x>4，
而大于4的数只有6.
故选D.
如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了四边形ABCD的两条边AB与BC，且四边形ABCD是一个轴对称图形，其对称轴为直线AC.
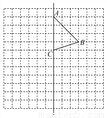
(1)试在图中标出点D，并画出该四边形的另两条边；
(2)将四边形ABCD向下平移5个单位，画出平移后得到的四边形A′B′C′D′.
（1）见解析；（2）见解析
【解析】试题分析：（1）画出点B关于直线AC的对称点D即可解决问题．
（2）将四边形ABCD各个顶点向下平移5个单位即可得到四边形A′B′C′D′．
试题解析：
【解析】
（1）点D以及四边形ABCD另两条边如图所示：
（2）得到的四边形A′B′C′D′如图所示． 已知a+b=-5,ab=7,求a2+b2的值.
11
【解析】试题分析：根据完全平方公式的变形进行计算即可．
试题解析：【解析】
因为a+b=-5，ab=7，
所以a2+b2=（a+b）2-2ab=（-5）2-2×7=11． 请阅读求绝对值不等式|x|＜3和|x|＞3的解集的过程：
因为|x|＜3，从如图1所示的数轴上看：大于-3而小于3的数的绝对值是小于3的，所以|x|＜3的解集是-3＜x＜3；
因为|x|＞3，从如图2所示的数轴上看：小大于-3的数和大于3的数的绝对值是大于3的，所以|x|＞3的解集是x＜-3或x＞3．
解答下面的问题：
（1）不等式|x|＜a（a＞0）的解集为______；不等式|x|＞a（a＞0）的解集为______．
（2）解不等式|x-5|＜3；
（3）解不等式|x-3|＞5．
（1）-a＜x＜a；x＞a或x＜-a．（2）2＜x＜8；（3）x＞8或x＜-2．
【解析】分析：(1)根据题中所给出的例子进行解答即可;(2)根据题中所给的实例列出关于x的不等式组,求出其解集即可.
本题解析： (1)不等式|x|＜a(a＞0)的解集为－a＜x＜a；不等式|x|＞a(a＞0)的解集为x＞a或x＜－a；
(2)|x－5|＜3，由(1)可知－3＜x－5＜3，∴2＜x＜... 对于解不等式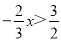
，正确的结果是（ ）
A．x＜
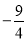B．x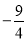＞ C．x＞-1 D．x＜-1
A．
【解析】
试题分析：先去分母得，-4x＞9，再把x的系数化为1得，x＜．
故选A． 当x 时，代数式2x－3的值是正数.
＞
【解析】
试题分析：先由题意列出不等式，再根据不等式的基本性质即可得到结果。
由题意得2x－3＞0，解得x＞. 若m＜n，比较下列各式的大小：
（1）m－3______n－3 （2）－5m______－5n （3）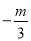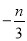
______
（4）3－m______2－n (5)0_____m－n （6）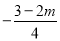
_____
< > > > > <
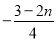
【解析】(1)m如图，△ABC中，AB=AC，AD是∠BAC的平分线．已知AB=5，AD=3，则BC的长为（ ）
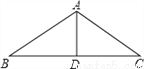
A. 5 B. 6 C. 8 D. 10
C
【解析】因为AB＝AC，AD是∠BAC的平分线，所以BC=2BD.
因为BD＝4，所以BC=2BD=2×4=8.
故选C. 如图，在△ABC中，已知∠C＝90°，AC=4，BC=3，那么下列结论不正确的是（ ）
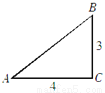
A. sinA=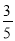
B. cosA=
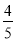C. tanA=
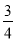D. cosB=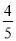
D
【解析】∵∠C＝90°，AC=4，BC=3，∴AB==5，
∴sinA==，cosA== ， tanA== ， cosB==，
故选D.