题目内容
如果t＞0，那么a＋t与a的大小关系是（ ）
A、a＋t＞a B、a＋t＜a C、a＋t≥a D、不能确定
A
【解析】
试题分析：根据不等式的基本性质即可得到结果.
t＞0，
∴a＋t＞a，
故选A.
练习册系列答案
口算能手系列答案
相关题目
用科学计算器计算：8cos31°+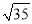
=_________
12.77
【解析】试题分析：8cos31°+=8×0.857+5.916=6.856+5.916=12.772≈12.77，
故答案为12.77． 请阅读求绝对值不等式|x|＜3和|x|＞3的解集的过程：
因为|x|＜3，从如图1所示的数轴上看：大于-3而小于3的数的绝对值是小于3的，所以|x|＜3的解集是-3＜x＜3；
因为|x|＞3，从如图2所示的数轴上看：小大于-3的数和大于3的数的绝对值是大于3的，所以|x|＞3的解集是x＜-3或x＞3．
解答下面的问题：
（1）不等式|x|＜a（a＞0）的解集为______；不等式|x|＞a（a＞0）的解集为______．
（2）解不等式|x-5|＜3；
（3）解不等式|x-3|＞5．
（1）-a＜x＜a；x＞a或x＜-a．（2）2＜x＜8；（3）x＞8或x＜-2．
【解析】分析：(1)根据题中所给出的例子进行解答即可;(2)根据题中所给的实例列出关于x的不等式组,求出其解集即可.
本题解析： (1)不等式|x|＜a(a＞0)的解集为－a＜x＜a；不等式|x|＞a(a＞0)的解集为x＞a或x＜－a；
(2)|x－5|＜3，由(1)可知－3＜x－5＜3，∴2＜x＜... 当x 时，代数式2x－3的值是正数.
＞
【解析】
试题分析：先由题意列出不等式，再根据不等式的基本性质即可得到结果。
由题意得2x－3＞0，解得x＞. 若m＜n，比较下列各式的大小：
（1）m－3______n－3 （2）－5m______－5n （3）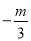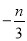
______
（4）3－m______2－n (5)0_____m－n （6）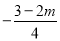
_____
< > > > > <
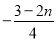
【解析】(1)m如图，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13.求四边形ABCD的面积．
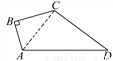
36.
【解析】试题分析：连接AC，在直角三角形ABC中，由AB及BC的长，利用勾股定理求出AC的长，再由AD及CD的长，利用勾股定理的逆定理得到三角形ACD为直角三角形，根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积，即可求出四边形的面积．
试题解析：【解析】
连接AC．如图所示：
∵∠B=90°，∴△ABC为直角三角形．又∵AB=3，BC=4，∴根... 如图，△ABC中，AB=AC，AD是∠BAC的平分线．已知AB=5，AD=3，则BC的长为（ ）
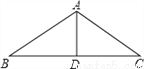
A. 5 B. 6 C. 8 D. 10
C
【解析】因为AB＝AC，AD是∠BAC的平分线，所以BC=2BD.
因为BD＝4，所以BC=2BD=2×4=8.
故选C. 如图，BC＝32cm，DE是AB的垂直平分线，D是垂足，DE交BC于E，AC＝18cm，则△AEC的周长为___cm.
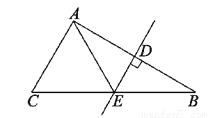
50
【解析】∵DE是AB的垂直平分线，
∴AE=BE．
∴△AEC的周长=AC+CE+AE=AC+BC=18+32=50（cm），
故答案为：50． 在△ABC中，∠C＝90°，∠A，∠B，∠C所对的边分别为a，b，c.
(1)已知c＝8
，∠A＝60°，求∠B，a，b；
(2)已知a＝3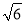
，∠A＝45°，求∠B，b，c.
(1)∠B＝30°，a＝12，b＝4；(2)∠B＝45°，b＝3，c＝6.
【解析】试题分析：（1）根据直角三角形两锐角互余求得∠B的度数，再根据30度角所对直角边等于斜边一半求得b，再根据勾股定理求得a即可；
（2）先根据直角三角形两锐角互余求得∠B=45°，从而得到b=a，再利用勾股定理即可求得c.
试题解析：（1）∵∠C=90°，∠A=60°，∴∠B=90°-∠A=30°，...