题目内容
5．如果等腰直角三角形ABC的面积是18cm，那么它的周长是12+6$\sqrt{2}$cm．分析 先根据等腰直角三角形的面积公式，求出两直角边的长，然后由勾股定理可求斜边的长，进而可求△ABC的周长．
解答 解：如图所示，∠C=90°，AB=BC，
∵S△ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}AC$2=18，
∴AC=6，
∴BC=6，
由勾股定理得：
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=6$\sqrt{2}$，
∴△ABC的周长=AC+BC+AB=（12+6$\sqrt{2}$）cm．
故答案为：12+6$\sqrt{2}$．
点评 此题考查了等腰直角三角形的面积公式与周长公式，解题的关键是：先根据等腰直角三角形的面积公式，求出两直角边的长．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
20．
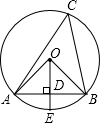如图，AB是⊙O的弦，OD⊥AB于D交⊙O于E，则下列说法错误的是（ ）
如图，AB是⊙O的弦，OD⊥AB于D交⊙O于E，则下列说法错误的是（ ）| A． | ∠ACB=∠AOE | B． | AD=BD | C． | S△AOB=$\frac{1}{2}$S△ABC | D． | AE=BE |
13．问题情境
初次见面，通常以握手示礼，适当的握手时间与力度，会让人有股舒服亲切的感受．9月1日开学时，老师为了让全班新同学互相认识，请班上41位同学彼此握手为礼，并同时彼此介绍自己．在一阵喧哗后，同学完成工作．老师提出一个问题：“谁知道，刚才全班同学总共握手几次？”小聪同学举手抢答说820次，他说的对不对？
探索研究
其实要解决握手问题，可以作以下的分析：假若两点代表两个人，连接两点的线段数目，就表示握手的次数． 我们可以作一个由点和线段组成的图来分析一下
因此，n个人握手总次为P=1+2+3…+（n+1）=$\frac{n（n-1）}{2}$
解决问题
班上41位同学彼此握手为礼，他们共握手多少次？小聪同学说的对不对？
问题拓展
请你用仿照上述方法来研究平面内n条直线最多有多少个交点？请你完成下表：
因此，平面内n条直线最多交点的个数为$\frac{{n（{n-1}）}}{2}$．
初次见面，通常以握手示礼，适当的握手时间与力度，会让人有股舒服亲切的感受．9月1日开学时，老师为了让全班新同学互相认识，请班上41位同学彼此握手为礼，并同时彼此介绍自己．在一阵喧哗后，同学完成工作．老师提出一个问题：“谁知道，刚才全班同学总共握手几次？”小聪同学举手抢答说820次，他说的对不对？
探索研究
其实要解决握手问题，可以作以下的分析：假若两点代表两个人，连接两点的线段数目，就表示握手的次数． 我们可以作一个由点和线段组成的图来分析一下
| 握手图标 | 握手人数 | 握手次数 |
 | 2 | 1 |
 | 3 | 3=1+2 |
 | 4 | 6=1+2+3 |
 | 5 | 10=1+2+3+4 |
| … | … | … |
| … | N | P=1+2+3+…+（n+1） |
解决问题
班上41位同学彼此握手为礼，他们共握手多少次？小聪同学说的对不对？
问题拓展
请你用仿照上述方法来研究平面内n条直线最多有多少个交点？请你完成下表：
| 图标 | 直线条数 | 交点个数 |
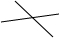 | 2 | 1 |
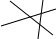 | 3 | 3=1+2 |
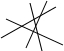 | 4 | |
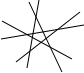 | 5 | |
| … | … | … |
| … | n |
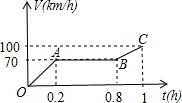一辆摩托车从起点出发沿笔直的赛道向终点行驶，行驶中的速度V（km/h）与时间t（h）的关系部分信息如图所示，根据图象有下列说法：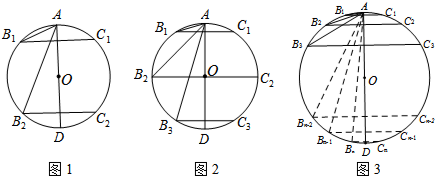
…
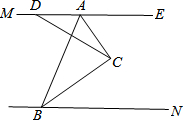如图，已知MA∥NB，CA平分∠BAE，CB平分∠ABN，点D是射线AM上一动点，连DC，当D点在射线AM（不包括A点）上滑动时，∠ADC+∠ACD+ABC的度数是否发生变化？若不变，说明理由，并求出度数．