题目内容
14.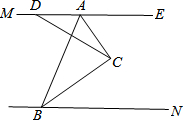 如图,已知MA∥NB,CA平分∠BAE,CB平分∠ABN,点D是射线AM上一动点,连DC,当D点在射线AM(不包括A点)上滑动时,∠ADC+∠ACD+ABC的度数是否发生变化?若不变,说明理由,并求出度数.
如图,已知MA∥NB,CA平分∠BAE,CB平分∠ABN,点D是射线AM上一动点,连DC,当D点在射线AM(不包括A点)上滑动时,∠ADC+∠ACD+ABC的度数是否发生变化?若不变,说明理由,并求出度数.
分析 先根据平行线的性质得出∠EAB+∠ABN=180°,再由CA平分∠BAE,CB平分∠ABN得出∠EAC=$\frac{1}{2}$∠EAB,∠ABC=$\frac{1}{2}$∠ABN,故可得出∠EAC+∠ABC的度数,再根据三角形外角的性质得出∠EAC=∠ADC+∠ACD,由此可得出结论.
解答 解:不变.∠ADC+∠ACD+ABC=90°.
理由:∵MA∥NB,
∴∠EAB+∠ABN=180°.
∵CA平分∠BAE,CB平分∠ABN,
∴∠EAC=$\frac{1}{2}$∠EAB,∠ABC=$\frac{1}{2}$∠ABN,
∴∠EAC+∠ABC=$\frac{1}{2}$(∠EAB+∠ABN)=90°.
∵∠EAC是△ACD的外角,
∴∠EAC=∠ADC+∠ACD,
∴∠ADC+∠ACD+ABC=∠EAC+∠ABC=90°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
相关题目
3.一汽车租赁公司拥有某种型号的汽车100辆,公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如表关系:
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式
(2)已知租出的车每辆每月需要维护费150元,未租出的车辆每月需要维护费50元,当租金定为3500元时,试求公司月收益为多少?
(3)根据市场调查报告,公司需要使每月出租的车辆不低于80辆,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
| x | 3000 | 3050 | 3100 | 3150 | 3200 | 3250 | 3300 |
| y | 100 | 99 | 98 | 97 | 96 | 95 | 94 |
(2)已知租出的车每辆每月需要维护费150元,未租出的车辆每月需要维护费50元,当租金定为3500元时,试求公司月收益为多少?
(3)根据市场调查报告,公司需要使每月出租的车辆不低于80辆,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
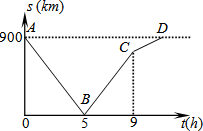 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶.设行驶时间为t(h),两车之间的距离为s(km),图中折线A-B-C-D表示s与t之间的函数关系.
一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶.设行驶时间为t(h),两车之间的距离为s(km),图中折线A-B-C-D表示s与t之间的函数关系.